Question Number 125437 by SOMEDAVONG last updated on 11/Dec/20
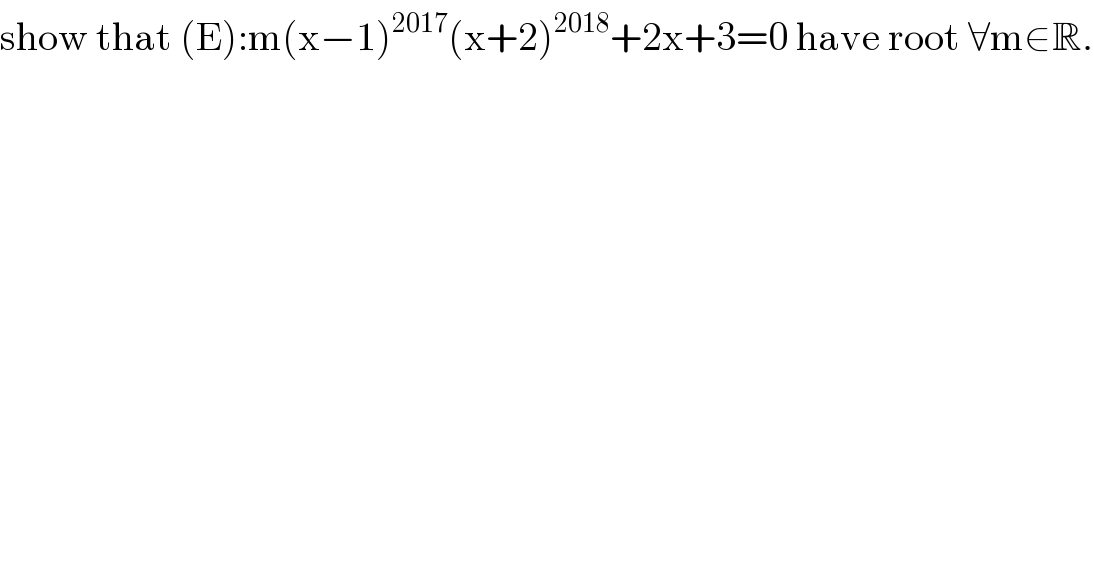
$$\mathrm{show}\:\mathrm{that}\:\left(\mathrm{E}\right):\mathrm{m}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2017}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2018}} +\mathrm{2x}+\mathrm{3}=\mathrm{0}\:\mathrm{have}\:\mathrm{root}\:\forall\mathrm{m}\in\mathbb{R}. \\ $$
Commented by Snail last updated on 11/Dec/20
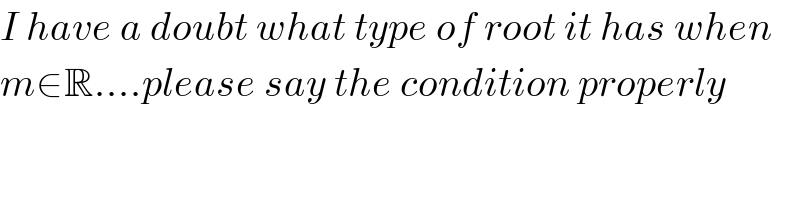
$${I}\:{have}\:{a}\:{doubt}\:{what}\:{type}\:{of}\:{root}\:{it}\:{has}\:{when}\: \\ $$$${m}\in\mathbb{R}….{please}\:{say}\:{the}\:{condition}\:{properly} \\ $$
