Question Number 151744 by mnjuly1970 last updated on 22/Aug/21
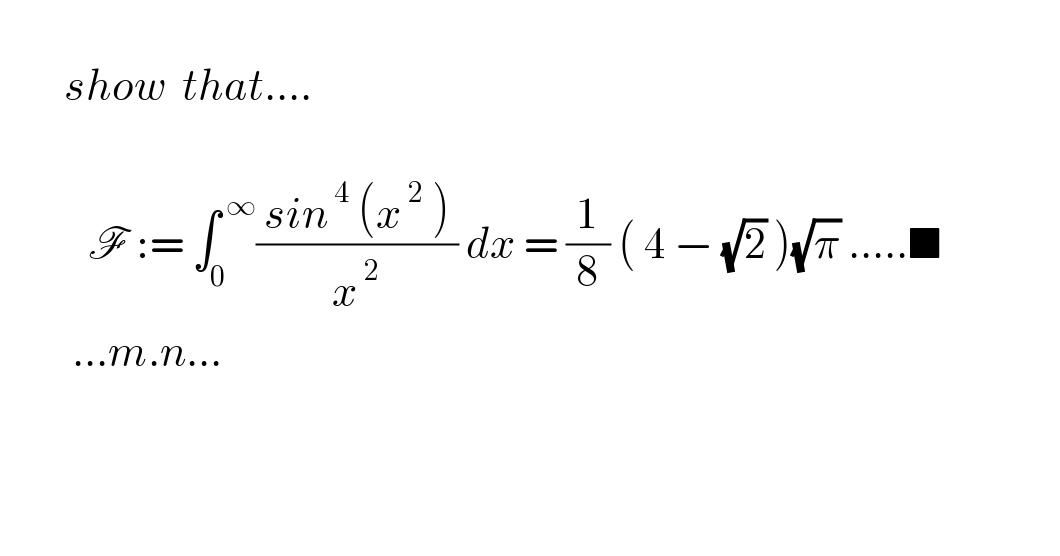
$$ \\ $$$$\:\:\:\:\:\:\:\:{show}\:\:{that}…. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathscr{F}\::=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}^{\:\mathrm{4}} \:\left({x}^{\:\mathrm{2}} \:\right)\:}{{x}^{\:\mathrm{2}} }\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\:\left(\:\mathrm{4}\:−\:\sqrt{\mathrm{2}}\:\right)\sqrt{\pi}\:…..\blacksquare\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:…{m}.{n}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by mindispower last updated on 22/Aug/21
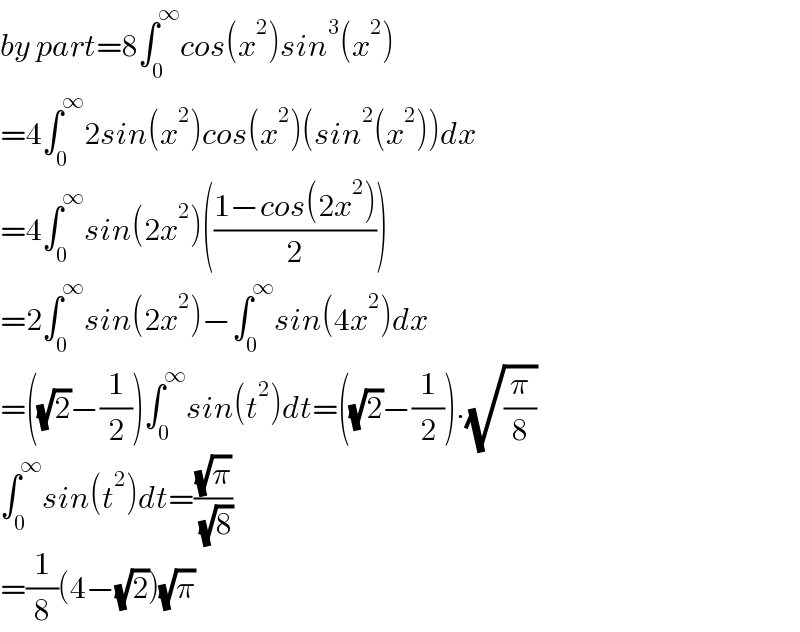
$${by}\:{part}=\mathrm{8}\int_{\mathrm{0}} ^{\infty} {cos}\left({x}^{\mathrm{2}} \right){sin}^{\mathrm{3}} \left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \mathrm{2}{sin}\left({x}^{\mathrm{2}} \right){cos}\left({x}^{\mathrm{2}} \right)\left({sin}^{\mathrm{2}} \left({x}^{\mathrm{2}} \right)\right){dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {sin}\left(\mathrm{2}{x}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {sin}\left(\mathrm{2}{x}^{\mathrm{2}} \right)−\int_{\mathrm{0}} ^{\infty} {sin}\left(\mathrm{4}{x}^{\mathrm{2}} \right){dx} \\ $$$$=\left(\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\int_{\mathrm{0}} ^{\infty} {sin}\left({t}^{\mathrm{2}} \right){dt}=\left(\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\right).\sqrt{\frac{\pi}{\mathrm{8}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {sin}\left({t}^{\mathrm{2}} \right){dt}=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{8}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{4}−\sqrt{\mathrm{2}}\right)\sqrt{\pi} \\ $$
Commented by mnjuly1970 last updated on 23/Aug/21
$${mercey}\:{sir}\:{power}… \\ $$
