Question Number 18652 by Tinkutara last updated on 26/Jul/17
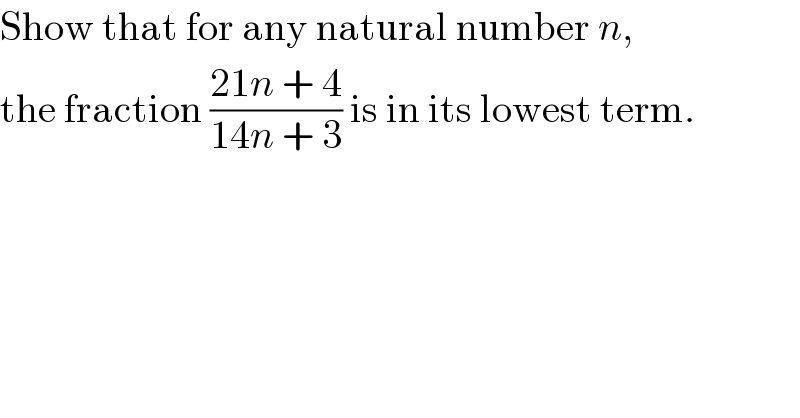
$$\mathrm{Show}\:\mathrm{that}\:\mathrm{for}\:\mathrm{any}\:\mathrm{natural}\:\mathrm{number}\:{n}, \\ $$$$\mathrm{the}\:\mathrm{fraction}\:\frac{\mathrm{21}{n}\:+\:\mathrm{4}}{\mathrm{14}{n}\:+\:\mathrm{3}}\:\mathrm{is}\:\mathrm{in}\:\mathrm{its}\:\mathrm{lowest}\:\mathrm{term}. \\ $$
Answered by diofanto last updated on 27/Jul/17

$$\mathrm{Lets}\:\mathrm{prove}\:\mathrm{by}\:\mathrm{contradiction}. \\ $$$$\mathrm{Suppose}\:\mathrm{there}\:\mathrm{is}\:{d}\:>\:\mathrm{1}\:\mathrm{such}\:\mathrm{that} \\ $$$${d}\:\mid\:\mathrm{21}{n}\:+\:\mathrm{4}\:\mathrm{and}\:{d}\:\mid\:\mathrm{14}{n}\:+\:\mathrm{3}. \\ $$$$\mathrm{Then}\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{true}\:\mathrm{that}: \\ $$$${d}\:\mid\:\mathrm{3}×\left(\mathrm{14}{n}+\mathrm{3}\right)−\mathrm{2}×\left(\mathrm{21}{n}+\mathrm{4}\right)\:\Leftrightarrow\:{d}\:\mid\:\mathrm{1} \\ $$$$\mathrm{But}\:{d}\:>\:\mathrm{1},\:\mathrm{contradiction}. \\ $$
Commented by Tinkutara last updated on 27/Jul/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{diofanto}\:\mathrm{Sir}! \\ $$
