Question Number 94861 by Ar Brandon last updated on 21/May/20
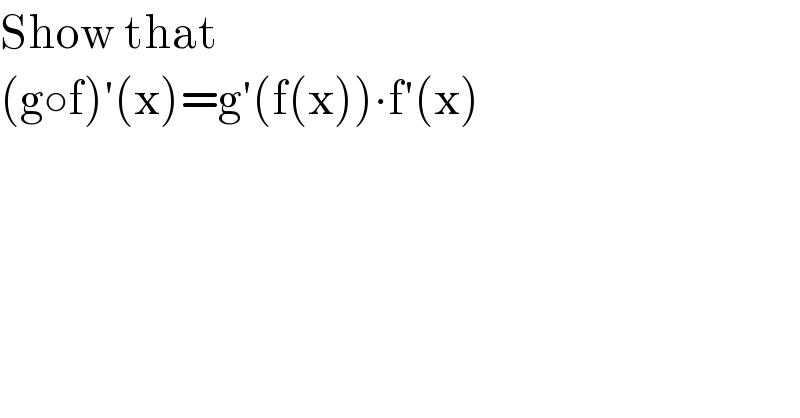
$$\mathrm{Show}\:\mathrm{that} \\ $$$$\left(\mathrm{g}\circ\mathrm{f}\right)'\left(\mathrm{x}\right)=\mathrm{g}'\left(\mathrm{f}\left(\mathrm{x}\right)\right)\centerdot\mathrm{f}'\left(\mathrm{x}\right) \\ $$
Commented by john santu last updated on 21/May/20
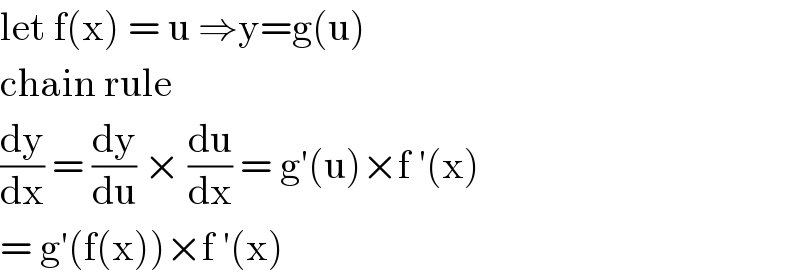
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{u}\:\Rightarrow\mathrm{y}=\mathrm{g}\left(\mathrm{u}\right) \\ $$$$\mathrm{chain}\:\mathrm{rule}\: \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{dy}}{\mathrm{du}}\:×\:\frac{\mathrm{du}}{\mathrm{dx}}\:=\:\mathrm{g}'\left(\mathrm{u}\right)×\mathrm{f}\:'\left(\mathrm{x}\right) \\ $$$$=\:\mathrm{g}'\left(\mathrm{f}\left(\mathrm{x}\right)\right)×\mathrm{f}\:'\left(\mathrm{x}\right) \\ $$
