Question Number 156270 by Tawa11 last updated on 09/Oct/21
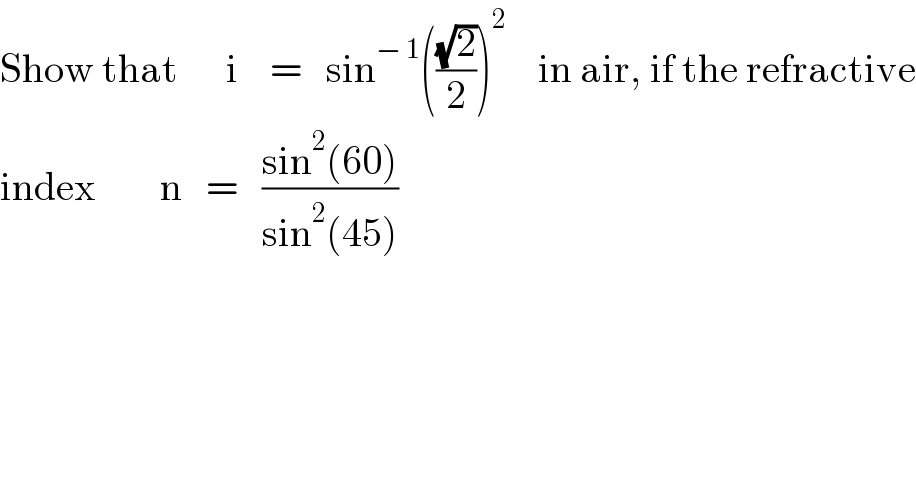
$$\mathrm{Show}\:\mathrm{that}\:\:\:\:\:\:\mathrm{i}\:\:\:\:=\:\:\:\mathrm{sin}^{−\:\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:\:\mathrm{in}\:\mathrm{air},\:\mathrm{if}\:\mathrm{the}\:\mathrm{refractive} \\ $$$$\mathrm{index}\:\:\:\:\:\:\:\:\mathrm{n}\:\:\:=\:\:\:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{60}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{45}\right)} \\ $$
Commented by Tawa11 last updated on 10/Oct/21
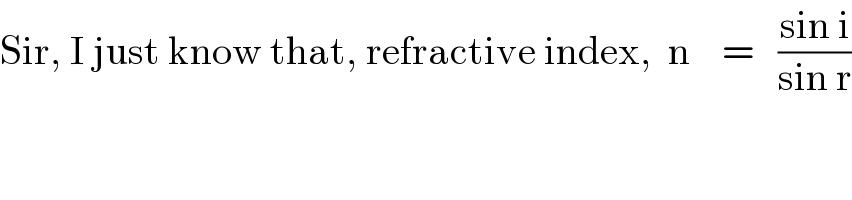
$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{just}\:\mathrm{know}\:\mathrm{that},\:\mathrm{refractive}\:\mathrm{index},\:\:\mathrm{n}\:\:\:\:=\:\:\:\frac{\mathrm{sin}\:\mathrm{i}}{\mathrm{sin}\:\mathrm{r}} \\ $$
Answered by ajfour last updated on 10/Oct/21
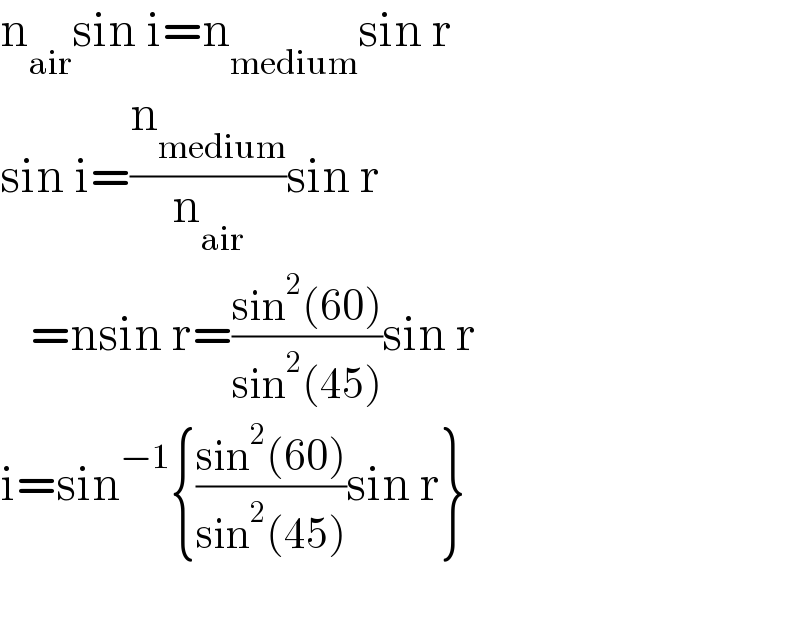
$$\mathrm{n}_{\mathrm{air}} \mathrm{sin}\:\mathrm{i}=\mathrm{n}_{\mathrm{medium}} \mathrm{sin}\:\mathrm{r} \\ $$$$\mathrm{sin}\:\mathrm{i}=\frac{\mathrm{n}_{\mathrm{medium}} }{\mathrm{n}_{\mathrm{air}} }\mathrm{sin}\:\mathrm{r} \\ $$$$\:\:\:=\mathrm{nsin}\:\mathrm{r}=\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{60}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{45}\right)}\mathrm{sin}\:\mathrm{r} \\ $$$$\mathrm{i}=\mathrm{sin}^{−\mathrm{1}} \left\{\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{60}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{45}\right)}\mathrm{sin}\:\mathrm{r}\right\} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 11/Oct/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
