Question Number 122651 by mathocean1 last updated on 18/Nov/20
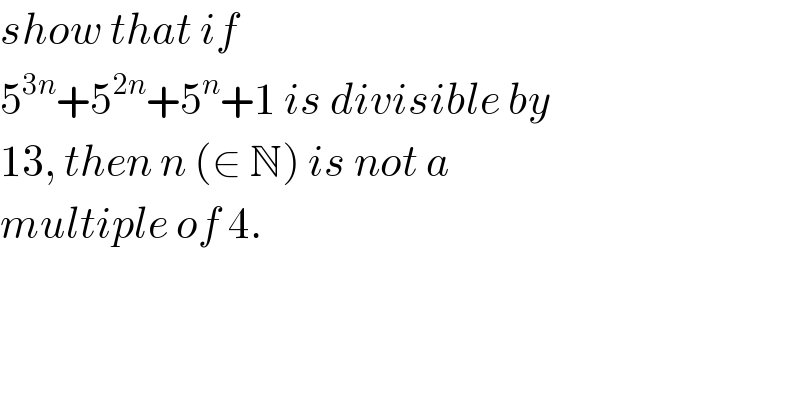
$${show}\:{that}\:{if}\: \\ $$$$\mathrm{5}^{\mathrm{3}{n}} +\mathrm{5}^{\mathrm{2}{n}} +\mathrm{5}^{{n}} +\mathrm{1}\:{is}\:{divisible}\:{by} \\ $$$$\mathrm{13},\:{then}\:{n}\:\left(\in\:\mathbb{N}\right)\:{is}\:{not}\:{a}\: \\ $$$${multiple}\:{of}\:\mathrm{4}. \\ $$
Answered by mindispower last updated on 18/Nov/20
![p⇒q⇔q^− ⇒p^− let n=4k 5^4 =625=13.48+1 5^4 =1[13] ⇒5^(3(4k)) +5^(2(4k)) +5^(4k) +1≡(1)^(3k) +1^(2k) +1^k +1≡4[13]≠0[13]](https://www.tinkutara.com/question/Q122657.png)
$${p}\Rightarrow{q}\Leftrightarrow\overset{−} {{q}}\Rightarrow\overset{−} {{p}} \\ $$$${let}\:{n}=\mathrm{4}{k} \\ $$$$\mathrm{5}^{\mathrm{4}} =\mathrm{625}=\mathrm{13}.\mathrm{48}+\mathrm{1} \\ $$$$\mathrm{5}^{\mathrm{4}} =\mathrm{1}\left[\mathrm{13}\right] \\ $$$$\Rightarrow\mathrm{5}^{\mathrm{3}\left(\mathrm{4}{k}\right)} +\mathrm{5}^{\mathrm{2}\left(\mathrm{4}{k}\right)} +\mathrm{5}^{\mathrm{4}{k}} +\mathrm{1}\equiv\left(\mathrm{1}\right)^{\mathrm{3}{k}} +\mathrm{1}^{\mathrm{2}{k}} +\mathrm{1}^{{k}} +\mathrm{1}\equiv\mathrm{4}\left[\mathrm{13}\right]\neq\mathrm{0}\left[\mathrm{13}\right] \\ $$
Commented by mathocean1 last updated on 18/Nov/20
$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$
