Question Number 95635 by Ar Brandon last updated on 26/May/20

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{if}\:\mathrm{a}\:\mathrm{function}\:\mathrm{is}\:\mathrm{even}\:\mathrm{and}\:\mathrm{derivable}\:\mathrm{then} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function}. \\ $$
Answered by mr W last updated on 26/May/20
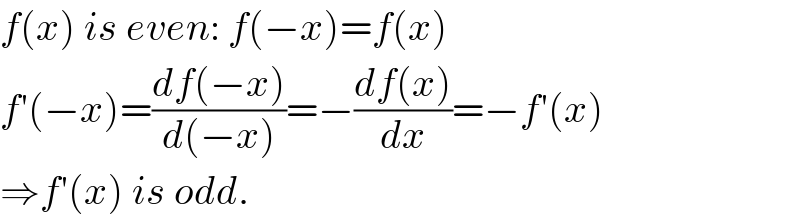
$${f}\left({x}\right)\:{is}\:{even}:\:{f}\left(−{x}\right)={f}\left({x}\right) \\ $$$${f}'\left(−{x}\right)=\frac{{df}\left(−{x}\right)}{{d}\left(−{x}\right)}=−\frac{{df}\left({x}\right)}{{dx}}=−{f}'\left({x}\right) \\ $$$$\Rightarrow{f}'\left({x}\right)\:{is}\:{odd}. \\ $$
