Question Number 156691 by mathocean1 last updated on 14/Oct/21
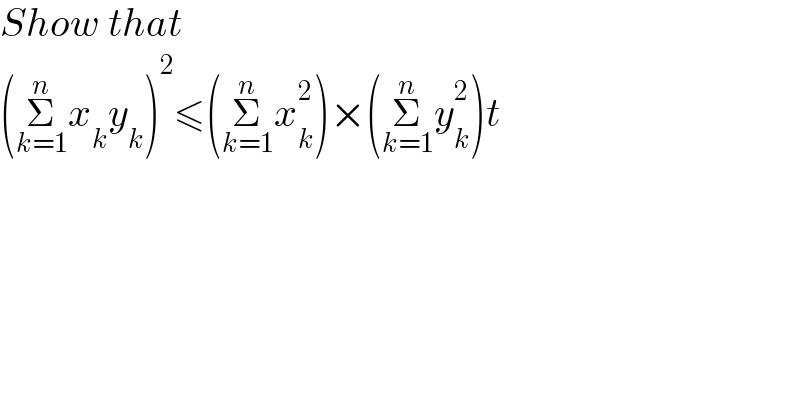
$${Show}\:{that} \\ $$$$\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} {y}_{{k}} \right)^{\mathrm{2}} \leqslant\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} ^{\mathrm{2}} \right)×\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{y}_{{k}} ^{\mathrm{2}} \right){t} \\ $$
Answered by puissant last updated on 14/Oct/21

$${P}\left(\lambda\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}_{{k}} +\lambda{y}_{{k}} \right)^{\mathrm{2}} \\ $$$$=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}_{{k}} ^{\mathrm{2}} +\mathrm{2}\lambda{x}_{{k}} {y}_{{k}} +\lambda^{\mathrm{2}} {y}_{{k}} ^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{P}\left(\lambda\right)=\lambda^{\mathrm{2}} \underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{y}_{{k}} ^{\mathrm{2}} +\mathrm{2}\lambda\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} {y}_{{k}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} ^{\mathrm{2}} \\ $$$${P}\left(\lambda\right)\geqslant\mathrm{0}\:\Rightarrow\:\Delta\leqslant\mathrm{0}.. \\ $$$$\Delta=\mathrm{4}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} {y}_{{k}} \right)^{\mathrm{2}} −\:\mathrm{4}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} ^{\mathrm{2}} \right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{y}_{{k}} ^{\mathrm{2}} \right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\:\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} {y}_{{k}} \right)^{\mathrm{2}} \leqslant\:\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} ^{\mathrm{2}} \right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{y}_{{k}} ^{\mathrm{2}} \right) \\ $$$$\left({Inequality}\:{of}\:{Cauchy}−{Schwartz}\right)… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:………….\mathscr{L}{e}\:{puissant}………… \\ $$
Commented by mathocean1 last updated on 22/Oct/21
$${thanks}\:{le}\:{puissant}. \\ $$
