Question Number 84859 by M±th+et£s last updated on 16/Mar/20
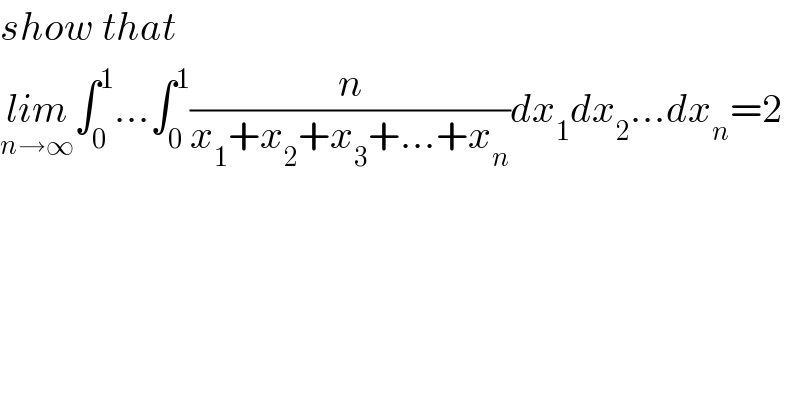
$${show}\:{that} \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} …\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{n}}{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +…+{x}_{{n}} }{dx}_{\mathrm{1}} {dx}_{\mathrm{2}} …{dx}_{{n}} =\mathrm{2}\: \\ $$
