Question Number 152247 by mathocean1 last updated on 26/Aug/21
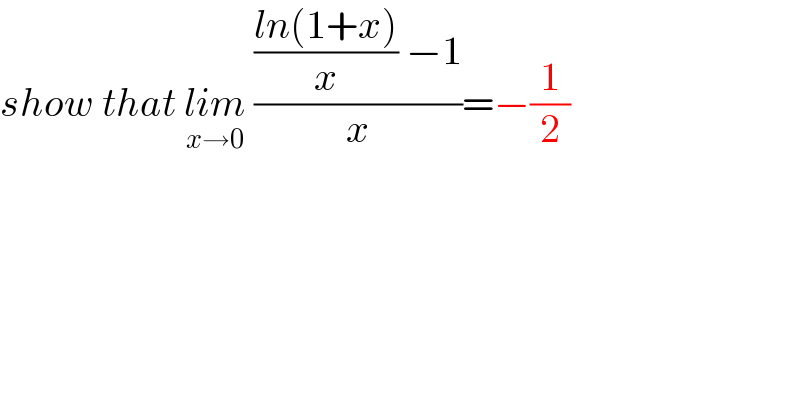
$${show}\:{that}\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}\:−\mathrm{1}}{{x}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 26/Aug/21
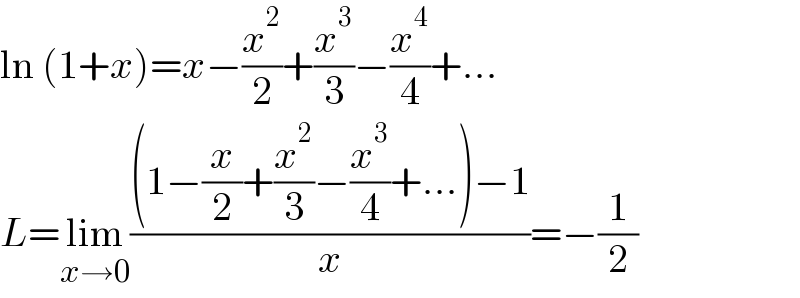
$$\mathrm{ln}\:\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+… \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+…\right)−\mathrm{1}}{{x}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by peter frank last updated on 27/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathocean1 last updated on 26/Aug/21

$${Please}\:{sir}\:{can}\:{you}\:{explain}\:{or}\:{find}\: \\ $$$${another}\:{way}\:{to}\:{calculate}\:{it}?\:{seriously} \\ $$$${i}\:{don}'{t}\:{understand}\:{even}\:{the}\:{first}\:{line} \\ $$$$:\:{i}\:{have}\:{just}\:{finished}\:{my}\:{studies}\:{in} \\ $$$${high}\:{scool}…{so}… \\ $$
Commented by mr W last updated on 26/Aug/21
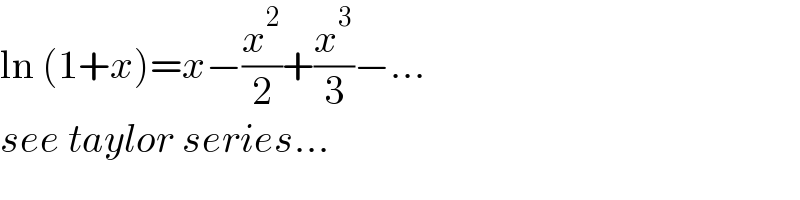
$$\mathrm{ln}\:\left(\mathrm{1}+{x}\right)={x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−… \\ $$$${see}\:{taylor}\:{series}… \\ $$
Commented by mr W last updated on 26/Aug/21
https://en.m.wikipedia.org/wiki/Taylor_series
Answered by Mokmokhi last updated on 26/Aug/21
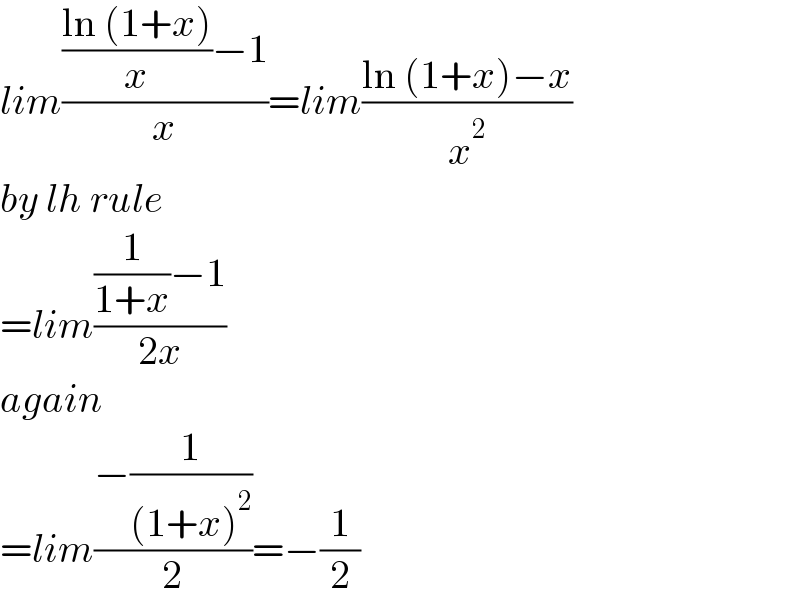
$${lim}\frac{\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)}{{x}}−\mathrm{1}}{{x}}={lim}\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)−{x}}{{x}^{\mathrm{2}} } \\ $$$${by}\:{lh}\:{rule} \\ $$$$={lim}\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}}−\mathrm{1}}{\mathrm{2}{x}} \\ $$$${again} \\ $$$$={lim}\frac{−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 26/Aug/21
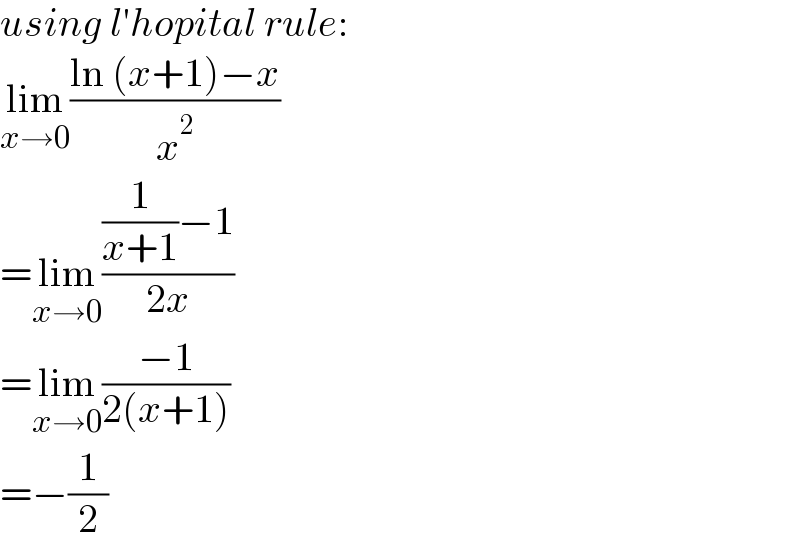
$${using}\:{l}'{hopital}\:{rule}: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left({x}+\mathrm{1}\right)−{x}}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{{x}+\mathrm{1}}−\mathrm{1}}{\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathocean1 last updated on 26/Aug/21
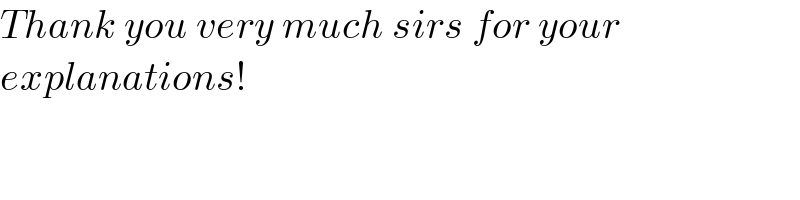
$${Thank}\:{you}\:{very}\:{much}\:{sirs}\:{for}\:{your} \\ $$$${explanations}! \\ $$
