Question Number 121051 by mathocean1 last updated on 05/Nov/20
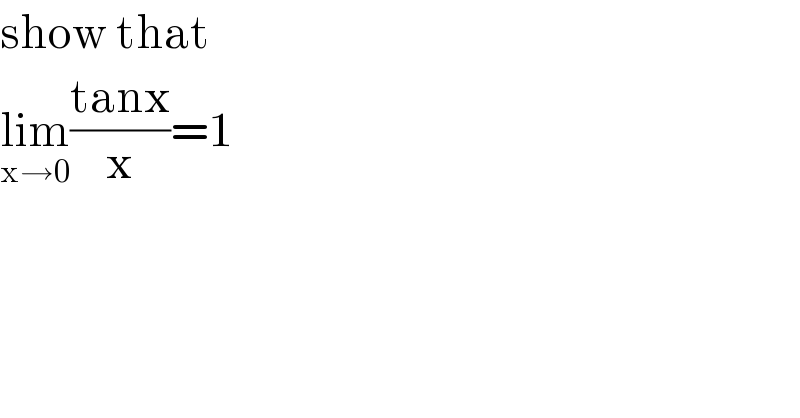
$$\mathrm{show}\:\mathrm{that} \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tanx}}{\mathrm{x}}=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Answered by 675480065 last updated on 05/Nov/20

$$\mathrm{as}\:\mathrm{x}\rightarrow\mathrm{0},\:\mathrm{tanx}\rightarrow\left(\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{0}\left(\mathrm{x}^{\mathrm{3}} \right)\right) \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tanx}}{\mathrm{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)}{\mathrm{x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)=\mathrm{1} \\ $$
Answered by physicstutes last updated on 05/Nov/20

$${x}\:\rightarrow\:\mathrm{0}\:,\:\mathrm{tan}\:{x}\:\rightarrow\:{x} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{{x}}\:=\:\mathrm{1}\:\mathrm{QED} \\ $$
