Menu Close

Show-that-n-1-1-n-H-n-n-2-5-8-3-m-n-

Tinku Tara 0 Comments
Pin




Question Number 166436 by mnjuly1970 last updated on 20/Feb/22
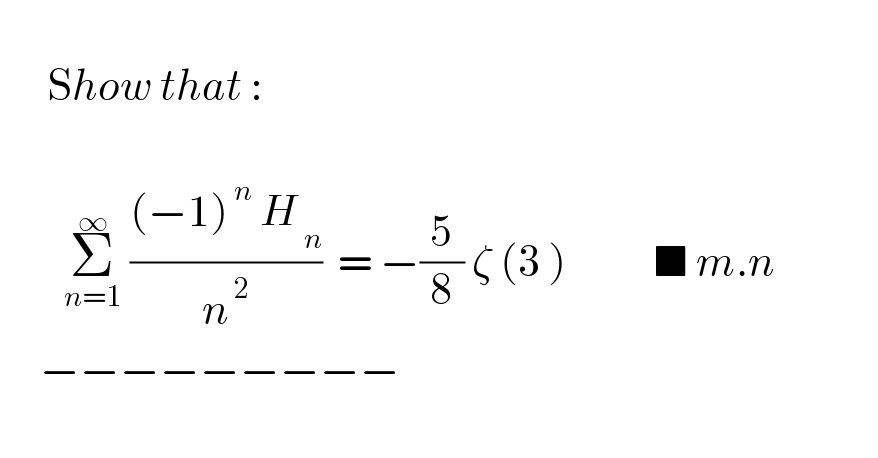
Show that : Σ_(n=1) ^∞ (((−1)^( n) H_( n) )/n^( 2) ) = −(5/8) ζ (3 ) ■ m.n −−−−−−−−−
$$ \\ $$$$\:\:\:\:\:\:\mathrm{S}{how}\:{that}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\:{n}} \:{H}_{\:{n}} }{{n}^{\:\mathrm{2}} }\:\:=\:−\frac{\mathrm{5}}{\mathrm{8}}\:\zeta\:\left(\mathrm{3}\:\right)\:\:\:\:\:\:\:\:\:\:\:\blacksquare\:{m}.{n}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:−−−−−−−−− \\ $$
Answered by qaz last updated on 20/Feb/22
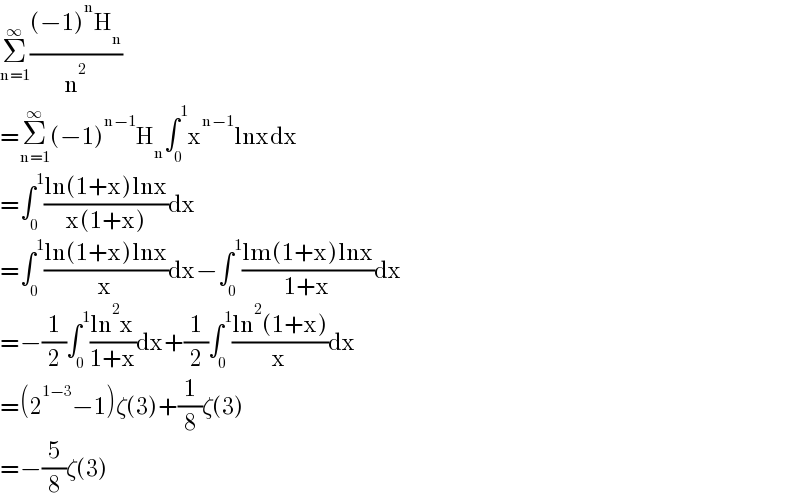
Σ_(n=1) ^∞ (((−1)^n H_n )/n^2 ) =Σ_(n=1) ^∞ (−1)^(n−1) H_n ∫_0 ^1 x^(n−1) lnxdx =∫_0 ^1 ((ln(1+x)lnx)/(x(1+x)))dx =∫_0 ^1 ((ln(1+x)lnx)/x)dx−∫_0 ^1 ((lm(1+x)lnx)/(1+x))dx =−(1/2)∫_0 ^1 ((ln^2 x)/(1+x))dx+(1/2)∫_0 ^1 ((ln^2 (1+x))/x)dx =(2^(1−3) −1)ζ(3)+(1/8)ζ(3) =−(5/8)ζ(3)
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{H}_{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{lnxdx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{lnx}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lm}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{lnx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{x}}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\left(\mathrm{2}^{\mathrm{1}−\mathrm{3}} −\mathrm{1}\right)\zeta\left(\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$$$=−\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$
Answered by mnjuly1970 last updated on 20/Feb/22
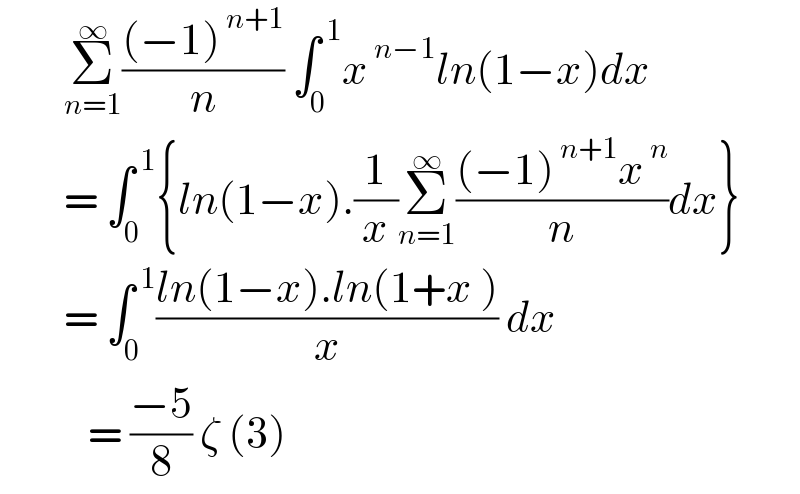
Σ_(n=1) ^∞ (((−1)^( n+1) )/n) ∫_0 ^( 1) x^( n−1) ln(1−x)dx = ∫_0 ^( 1) {ln(1−x).(1/x)Σ_(n=1) ^∞ (((−1)^( n+1) x^( n) )/n)dx} = ∫_0 ^( 1) ((ln(1−x).ln(1+x ))/x) dx = ((−5)/8) ζ (3)
$$\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}+\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\:{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{{ln}\left(\mathrm{1}−{x}\right).\frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}+\mathrm{1}} {x}^{\:{n}} }{{n}}{dx}\right\} \\ $$$$\:\:\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right).{ln}\left(\mathrm{1}+{x}\:\right)}{{x}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{5}}{\mathrm{8}}\:\zeta\:\left(\mathrm{3}\right)\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *