Menu Close

show-that-n-k-0-n-k-n-k-2-pi-2-6-

Tinku Tara 0 Comments
Pin




Question Number 83629 by M±th+et£s last updated on 04/Mar/20
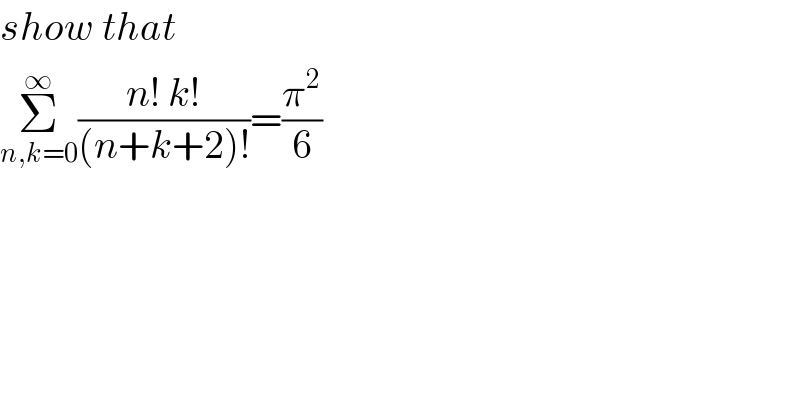
show that Σ_(n,k=0) ^∞ ((n! k!)/((n+k+2)!))=(π^2 /6)
$${show}\:{that} \\ $$$$\underset{{n},{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}!\:{k}!}{\left({n}+{k}+\mathrm{2}\right)!}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Answered by Kamel Kamel last updated on 04/Mar/20
S(x)=Σ_(n=0) ^(+∞) Σ_(k=0) ^(+∞) ((n!k!)/((n+k+2)!))x^(n+k+2) =Σ_(n=0) ^(+∞) Σ_(k=0) ^(+∞) ((Γ(n+1)Γ(k+1))/(Γ(n+k+2)(n+k+2)))x^(n+k+2) S′(x)=Σ_(n=0) ^(+∞) Σ_(k=0) ^(+∞) x^(n+k+1) ∫_0 ^1 t^n (1−t)^k dt =x∫_0 ^1 (1/(1−xt)) (1/(1−x(1−t)))dt (1/((1−xt)(1−x+xt)))=(1/(2−x))((1/(1−xt))+(1/(1−x+xt))) ∴ S′(x)=(1/(2−x))∫_0 ^1 ((1/(1−xt))+(1/(1−x+xt)))xdt=−(2/(2−x))Ln(1−x) =−(2/(2−x))Ln(1−x) ∴ S=−2∫_0 ^1 ((Ln(1−x))/(2−x))dx=^(t=2−x) − 2∫_1 ^2 ((Ln(t−1))/t)dt =^(z=(1/t)) −2∫_(1/2) ^1 ((Ln(1−z)−Ln(z))/z)dz =2(Li_2 (1)−Li_2 ((1/2)))−Ln^2 (2) Li_2 (1−x)+Li_2 (x)=(π^2 /6)−Ln(x)Ln(1−x) ∴Li_2 ((1/2))=(π^2 /(12))−(1/2)Ln^2 (2) So: S=2((π^2 /6)−(π^2 /(12))+(1/2)Ln^2 (2))−Ln^2 (2)=(π^2 /6)
$${S}\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{{n}!{k}!}{\left({n}+{k}+\mathrm{2}\right)!}{x}^{{n}+{k}+\mathrm{2}} =\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\Gamma\left({n}+\mathrm{1}\right)\Gamma\left({k}+\mathrm{1}\right)}{\Gamma\left({n}+{k}+\mathrm{2}\right)\left({n}+{k}+\mathrm{2}\right)}{x}^{{n}+{k}+\mathrm{2}} \\ $$$${S}'\left({x}\right)=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}{x}^{{n}+{k}+\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}} \left(\mathrm{1}−{t}\right)^{{k}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{xt}}\:\frac{\mathrm{1}}{\mathrm{1}−{x}\left(\mathrm{1}−{t}\right)}{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}−{xt}\right)\left(\mathrm{1}−{x}+{xt}\right)}=\frac{\mathrm{1}}{\mathrm{2}−{x}}\left(\frac{\mathrm{1}}{\mathrm{1}−{xt}}+\frac{\mathrm{1}}{\mathrm{1}−{x}+{xt}}\right) \\ $$$$\therefore\:{S}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}−{x}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}−{xt}}+\frac{\mathrm{1}}{\mathrm{1}−{x}+{xt}}\right){xdt}=−\frac{\mathrm{2}}{\mathrm{2}−{x}}{Ln}\left(\mathrm{1}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{2}}{\mathrm{2}−{x}}{Ln}\left(\mathrm{1}−{x}\right) \\ $$$$\therefore\:{S}=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left(\mathrm{1}−{x}\right)}{\mathrm{2}−{x}}{dx}\overset{{t}=\mathrm{2}−{x}} {=}−\:\:\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{Ln}\left({t}−\mathrm{1}\right)}{{t}}{dt} \\ $$$$\:\:\:\:\:\:\:\:\overset{{z}=\frac{\mathrm{1}}{{t}}} {=}\:\:−\mathrm{2}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \frac{{Ln}\left(\mathrm{1}−{z}\right)−{Ln}\left({z}\right)}{{z}}{dz} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left({Li}_{\mathrm{2}} \left(\mathrm{1}\right)−{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−{Ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$${Li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)+{Li}_{\mathrm{2}} \left({x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−{Ln}\left({x}\right){Ln}\left(\mathrm{1}−{x}\right) \\ $$$$\therefore{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}}{Ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$${So}:\:\:{S}=\mathrm{2}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{2}}{Ln}^{\mathrm{2}} \left(\mathrm{2}\right)\right)−{Ln}^{\mathrm{2}} \left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented by M±th+et£s last updated on 04/Mar/20
nice solution sir thank you
$${nice}\:{solution}\:{sir}\:{thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *