Question Number 115218 by Ar Brandon last updated on 24/Sep/20
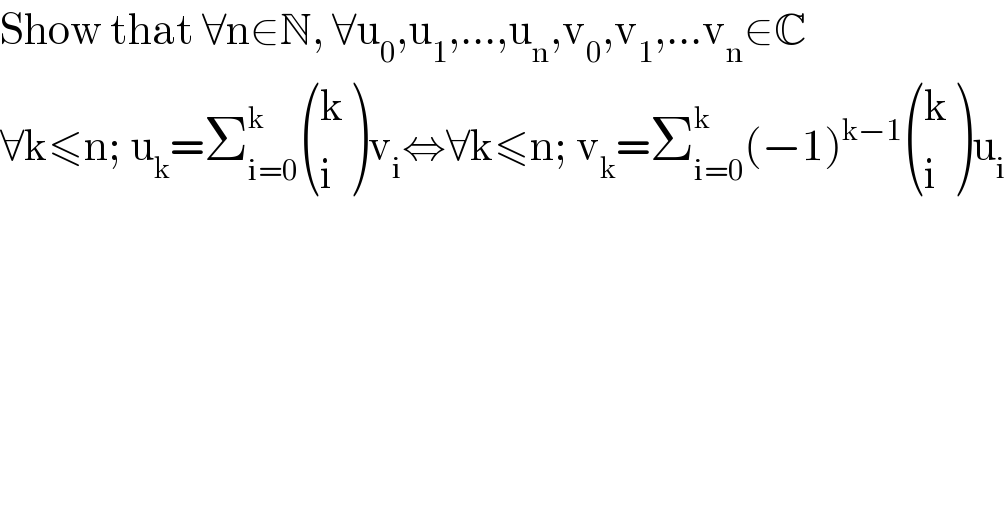
$$\mathrm{Show}\:\mathrm{that}\:\forall\mathrm{n}\in\mathbb{N},\:\forall\mathrm{u}_{\mathrm{0}} ,\mathrm{u}_{\mathrm{1}} ,…,\mathrm{u}_{\mathrm{n}} ,\mathrm{v}_{\mathrm{0}} ,\mathrm{v}_{\mathrm{1}} ,…\mathrm{v}_{\mathrm{n}} \in\mathbb{C} \\ $$$$\forall\mathrm{k}\leqslant\mathrm{n};\:\mathrm{u}_{\mathrm{k}} =\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{k}} \begin{pmatrix}{\mathrm{k}}\\{\mathrm{i}}\end{pmatrix}\mathrm{v}_{\mathrm{i}} \Leftrightarrow\forall\mathrm{k}\leqslant\mathrm{n};\:\mathrm{v}_{\mathrm{k}} =\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \begin{pmatrix}{\mathrm{k}}\\{\mathrm{i}}\end{pmatrix}\mathrm{u}_{\mathrm{i}} \\ $$
