Question Number 58246 by tanmay last updated on 20/Apr/19
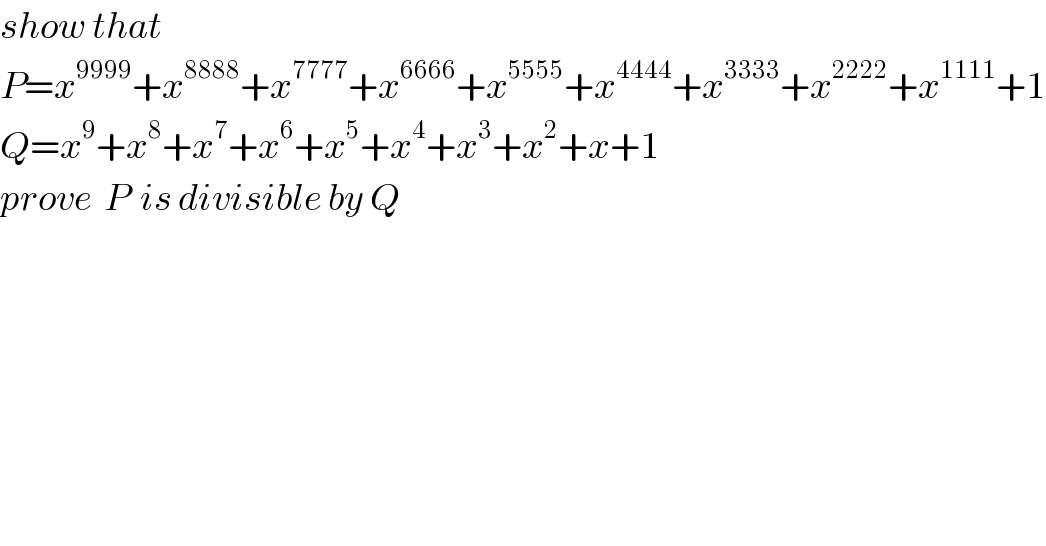
$${show}\:{that} \\ $$$${P}={x}^{\mathrm{9999}} +{x}^{\mathrm{8888}} +{x}^{\mathrm{7777}} +{x}^{\mathrm{6666}} +{x}^{\mathrm{5555}} +{x}^{\mathrm{4444}} +{x}^{\mathrm{3333}} +{x}^{\mathrm{2222}} +{x}^{\mathrm{1111}} +\mathrm{1} \\ $$$${Q}={x}^{\mathrm{9}} +{x}^{\mathrm{8}} +{x}^{\mathrm{7}} +{x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$$${prove}\:\:{P}\:\:{is}\:{divisible}\:{by}\:{Q} \\ $$
Answered by 2pac last updated on 25/Apr/19
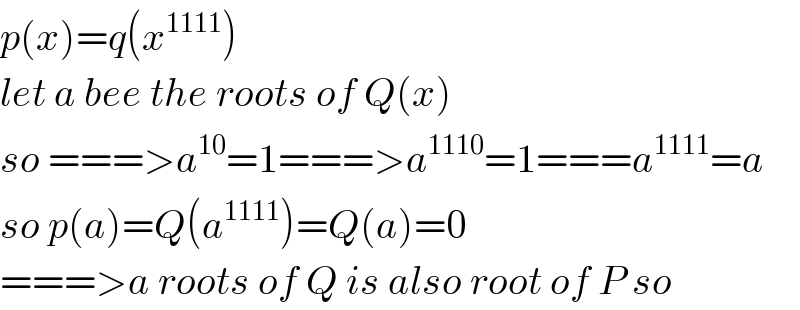
$${p}\left({x}\right)={q}\left({x}^{\mathrm{1111}} \right) \\ $$$${let}\:{a}\:{bee}\:{the}\:{roots}\:{of}\:{Q}\left({x}\right)\: \\ $$$${so}\:===>{a}^{\mathrm{10}} =\mathrm{1}===>{a}^{\mathrm{1110}} =\mathrm{1}==={a}^{\mathrm{1111}} ={a} \\ $$$${so}\:{p}\left({a}\right)={Q}\left({a}^{\mathrm{1111}} \right)={Q}\left({a}\right)=\mathrm{0} \\ $$$$===>{a}\:{roots}\:{of}\:{Q}\:{is}\:{also}\:{root}\:{of}\:{P}\:{so}\: \\ $$
