Question Number 97576 by Rio Michael last updated on 08/Jun/20
![Show that RE[(1/(1−z))]=(1/2) where z = cos θ + i sinθ](https://www.tinkutara.com/question/Q97576.png)
$$\:\mathrm{Show}\:\mathrm{that}\:{RE}\left[\frac{\mathrm{1}}{\mathrm{1}−{z}}\right]=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{where}\:{z}\:=\:\mathrm{cos}\:\theta\:+\:{i}\:\mathrm{sin}\theta \\ $$$$ \\ $$
Answered by smridha last updated on 08/Jun/20
![RE[(1/(1−e^(i𝛉) ))]=RE[((1+e^(i𝛉) )/(1−e^(2i𝛉) ))] RE[((e^(−i𝛉) +1)/(e^(−i𝛉) −e^(i𝛉) ))]=Re[(((cos𝛉−isinθ+1))/(−2isin𝛉))] =RE[((sin𝛉+i(cos𝛉+1))/(2sin𝛉))]=RE[(1/2)+i(((cos𝛉+1)/(2sinθ)))] =(1/2)](https://www.tinkutara.com/question/Q97584.png)
$$\boldsymbol{{RE}}\left[\frac{\mathrm{1}}{\mathrm{1}−\boldsymbol{{e}}^{\boldsymbol{{i}\theta}} }\right]=\boldsymbol{{RE}}\left[\frac{\mathrm{1}+{e}^{{i}\boldsymbol{\theta}} }{\mathrm{1}−{e}^{\mathrm{2}{i}\boldsymbol{\theta}} }\right] \\ $$$$\boldsymbol{{R}}{E}\left[\frac{{e}^{−{i}\boldsymbol{\theta}} +\mathrm{1}}{{e}^{−{i}\boldsymbol{\theta}} −{e}^{{i}\boldsymbol{\theta}} }\right]={Re}\left[\frac{\left({cos}\boldsymbol{\theta}−{isin}\theta+\mathrm{1}\right)}{−\mathrm{2}\boldsymbol{{isin}\theta}}\right] \\ $$$$=\boldsymbol{{RE}}\left[\frac{{sin}\boldsymbol{\theta}+{i}\left(\boldsymbol{{cos}\theta}+\mathrm{1}\right)}{\mathrm{2}\boldsymbol{{sin}\theta}}\right]=\boldsymbol{{RE}}\left[\frac{\mathrm{1}}{\mathrm{2}}+{i}\left(\frac{\boldsymbol{{cos}\theta}+\mathrm{1}}{\mathrm{2}{sin}\theta}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 08/Jun/20
$$\mathrm{really}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{this}\:\mathrm{sir}…\mathrm{can}\:\mathrm{you}\:\mathrm{please} \\ $$$$\mathrm{take}\:\mathrm{it}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step}? \\ $$
Commented by smridha last updated on 08/Jun/20

$$\boldsymbol{{from}}\:\boldsymbol{{which}}\:\boldsymbol{{step}}\:\boldsymbol{{you}}\:\boldsymbol{{get}}\:\boldsymbol{{puzzled}}? \\ $$$$\boldsymbol{{I}}\:\:\boldsymbol{{think}}\:\boldsymbol{{you}}\:\boldsymbol{{take}}\:\boldsymbol{{some}}\:\boldsymbol{{time}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{try}}\:\boldsymbol{{to}}\:\boldsymbol{{understand}}\:\boldsymbol{{slowly}}\: \\ $$$$\boldsymbol{{slowly}}…..\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{trick}}.. \\ $$
Commented by Rio Michael last updated on 08/Jun/20
$$\boldsymbol{\mathrm{am}}\:\boldsymbol{\mathrm{fine}}\:\boldsymbol{\mathrm{now}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{thanks}}. \\ $$
Answered by abdomathmax last updated on 08/Jun/20
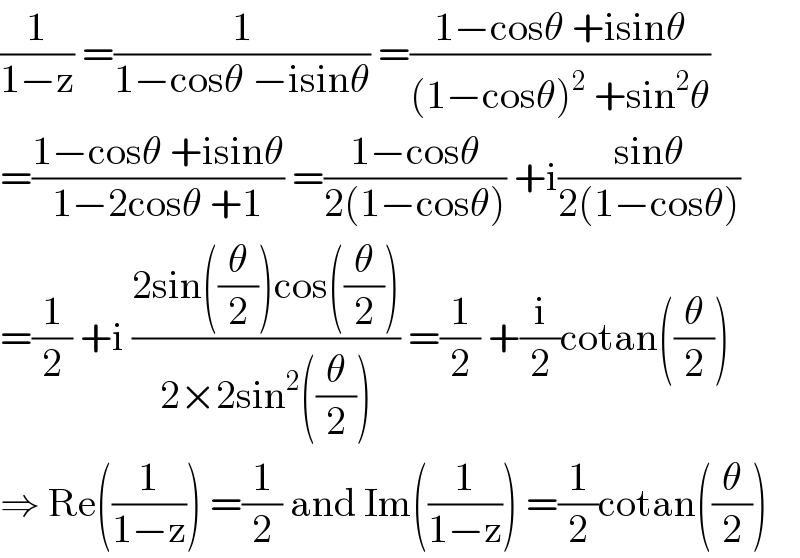
$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}\:=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}\theta\:−\mathrm{isin}\theta}\:=\frac{\mathrm{1}−\mathrm{cos}\theta\:+\mathrm{isin}\theta}{\left(\mathrm{1}−\mathrm{cos}\theta\right)^{\mathrm{2}} \:+\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\theta\:+\mathrm{isin}\theta}{\mathrm{1}−\mathrm{2cos}\theta\:+\mathrm{1}}\:=\frac{\mathrm{1}−\mathrm{cos}\theta}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\theta\right)}\:+\mathrm{i}\frac{\mathrm{sin}\theta}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\theta\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{i}\:\frac{\mathrm{2sin}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2}×\mathrm{2sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{i}}{\mathrm{2}}\mathrm{cotan}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{Re}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{Im}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cotan}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$
