Question Number 153409 by SOMEDAVONG last updated on 07/Sep/21
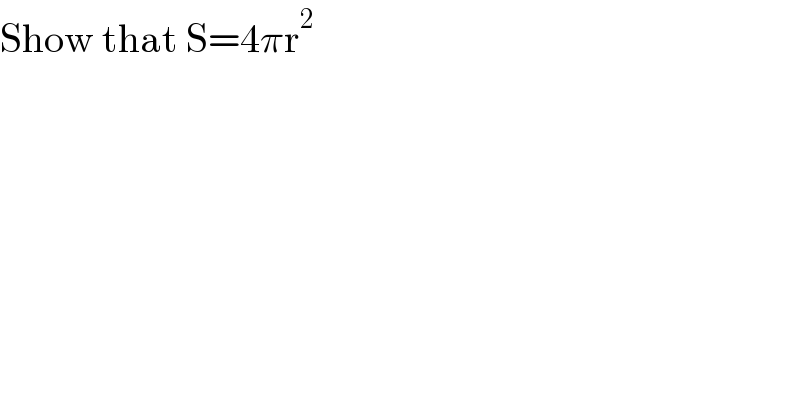
$$\mathrm{Show}\:\mathrm{that}\:\mathrm{S}=\mathrm{4}\pi\mathrm{r}^{\mathrm{2}} \\ $$
Answered by puissant last updated on 07/Sep/21
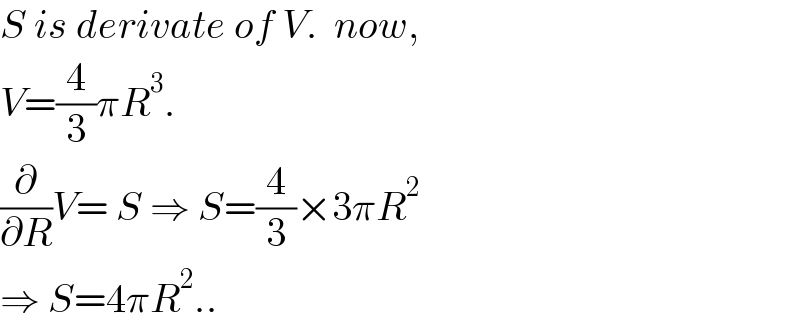
$${S}\:{is}\:{derivate}\:{of}\:{V}.\:\:{now},\: \\ $$$${V}=\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} . \\ $$$$\frac{\partial}{\partial{R}}{V}=\:{S}\:\Rightarrow\:{S}=\frac{\mathrm{4}}{\mathrm{3}}×\mathrm{3}\pi{R}^{\mathrm{2}} \\ $$$$\Rightarrow\:{S}=\mathrm{4}\pi{R}^{\mathrm{2}} .. \\ $$
Commented by puissant last updated on 07/Sep/21
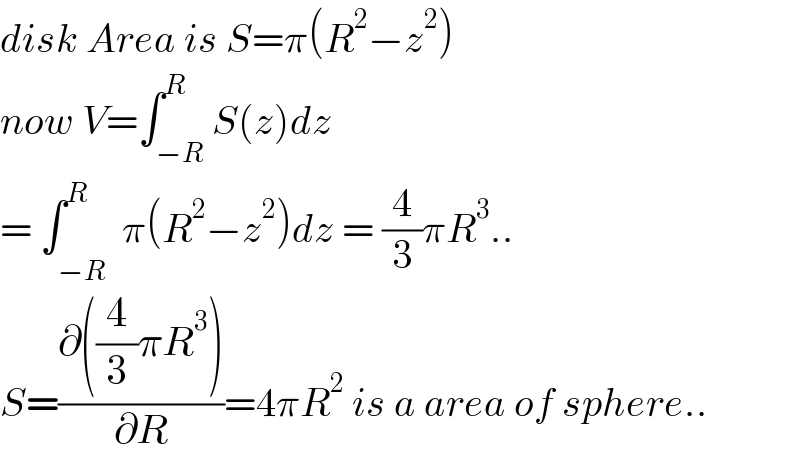
$${disk}\:{Area}\:{is}\:{S}=\pi\left({R}^{\mathrm{2}} −{z}^{\mathrm{2}} \right) \\ $$$${now}\:{V}=\int_{−{R}} ^{{R}} {S}\left({z}\right){dz} \\ $$$$=\:\int_{−{R}^{} } ^{{R}} \pi\left({R}^{\mathrm{2}} −{z}^{\mathrm{2}} \right){dz}\:=\:\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} .. \\ $$$${S}=\frac{\partial\left(\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} \right)}{\partial{R}}=\mathrm{4}\pi{R}^{\mathrm{2}} \:{is}\:{a}\:{area}\:{of}\:{sphere}.. \\ $$
Commented by MJS_new last updated on 07/Sep/21
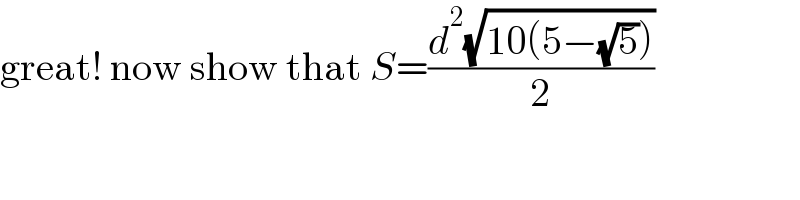
$$\mathrm{great}!\:\mathrm{now}\:\mathrm{show}\:\mathrm{that}\:{S}=\frac{{d}^{\mathrm{2}} \sqrt{\mathrm{10}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}}{\mathrm{2}} \\ $$
Commented by puissant last updated on 07/Sep/21

$${it}'{s}\:{weird} \\ $$
Commented by MJS_new last updated on 07/Sep/21

$$\mathrm{sorry}.\:\mathrm{for}\:\mathrm{me}\:\mathrm{it}\:\mathrm{seems}\:\mathrm{weird}\:\mathrm{to}\:\mathrm{answer}\:\mathrm{this} \\ $$$$\mathrm{question}\:\mathrm{and}\:\mathrm{similar}\:\mathrm{ones}.\:\mathrm{can}\:\mathrm{you}\:\mathrm{be}\:\mathrm{sure} \\ $$$${S}\:\mathrm{is}\:\mathrm{the}\:\mathrm{surface}\:\mathrm{of}\:\mathrm{a}\:\mathrm{sphere}?\:\mathrm{the}\:\mathrm{question}\:\mathrm{is} \\ $$$$\mathrm{not}\:\mathrm{complete}. \\ $$
Commented by puissant last updated on 07/Sep/21
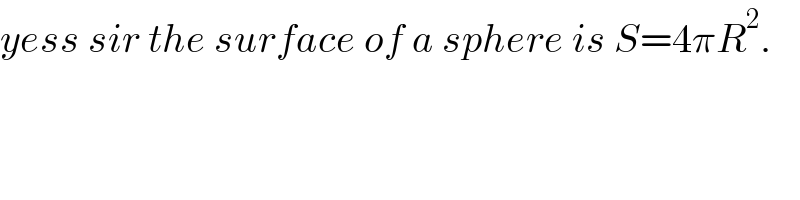
$${yess}\:{sir}\:{the}\:{surface}\:{of}\:{a}\:{sphere}\:{is}\:{S}=\mathrm{4}\pi{R}^{\mathrm{2}} . \\ $$
Commented by MJS_new last updated on 07/Sep/21
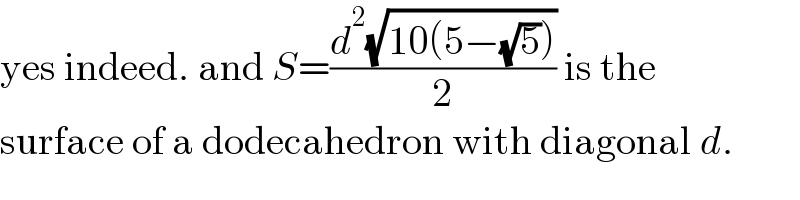
$$\mathrm{yes}\:\mathrm{indeed}.\:\mathrm{and}\:{S}=\frac{{d}^{\mathrm{2}} \sqrt{\mathrm{10}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}}{\mathrm{2}}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{surface}\:\mathrm{of}\:\mathrm{a}\:\mathrm{dodecahedron}\:\mathrm{with}\:\mathrm{diagonal}\:{d}. \\ $$
Commented by puissant last updated on 07/Sep/21
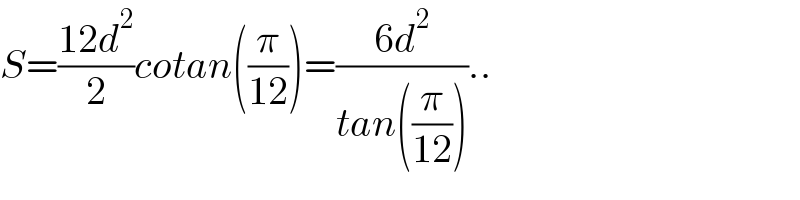
$${S}=\frac{\mathrm{12}{d}^{\mathrm{2}} }{\mathrm{2}}{cotan}\left(\frac{\pi}{\mathrm{12}}\right)=\frac{\mathrm{6}{d}^{\mathrm{2}} }{{tan}\left(\frac{\pi}{\mathrm{12}}\right)}.. \\ $$
Commented by prakash jain last updated on 07/Sep/21
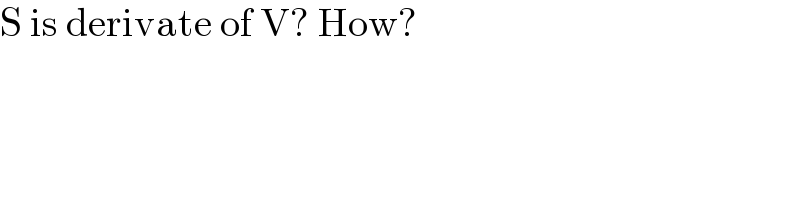
$$\mathrm{S}\:\mathrm{is}\:\mathrm{derivate}\:\mathrm{of}\:\mathrm{V}?\:\mathrm{How}? \\ $$
