Question Number 34066 by 5a3k last updated on 30/Apr/18
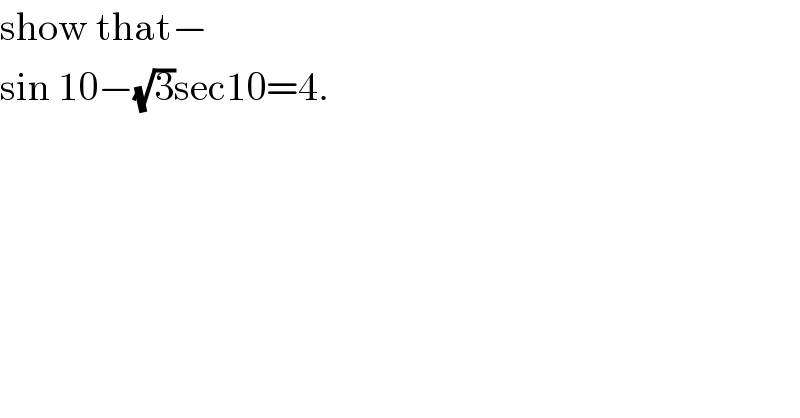
$$\mathrm{show}\:\mathrm{that}− \\ $$$$\mathrm{sin}\:\mathrm{10}−\sqrt{\mathrm{3}}\mathrm{sec10}=\mathrm{4}. \\ $$
Answered by math1967 last updated on 30/Apr/18

$${correct}\:{q}.\:{is}\:\frac{\mathrm{1}}{{sin}\mathrm{10}°}\:−\sqrt{\mathrm{3}\:\:\:}\:{sec}\mathrm{10}° \\ $$$$\frac{{cos}\mathrm{10}°−\sqrt{\mathrm{3}}\:{sin}\mathrm{10}}{{sin}\mathrm{10}{cos}\mathrm{10}\:\:} \\ $$$$\frac{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{10}−\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}{sin}\mathrm{10}\right)}{{sin}\mathrm{10}{cos}\mathrm{10}} \\ $$$$\frac{\mathrm{2}\left({sin}\mathrm{30}{cos}\mathrm{10}−{cos}\mathrm{30}{sin}\mathrm{10}\right)}{{sin}\mathrm{10}{cos}\mathrm{10}} \\ $$$$\frac{\mathrm{2}{sin}\left(\mathrm{30}−\mathrm{10}\right)}{{sin}\mathrm{10}{cos}\mathrm{10}}=\frac{\mathrm{4}{sin}\mathrm{20}}{\mathrm{2}{sin}\mathrm{10}{cos}\mathrm{10}}=\frac{\mathrm{4}{sin}\mathrm{20}}{{sin}\mathrm{20}} \\ $$$$=\mathrm{4} \\ $$$$ \\ $$
