Question Number 172026 by Mikenice last updated on 23/Jun/22
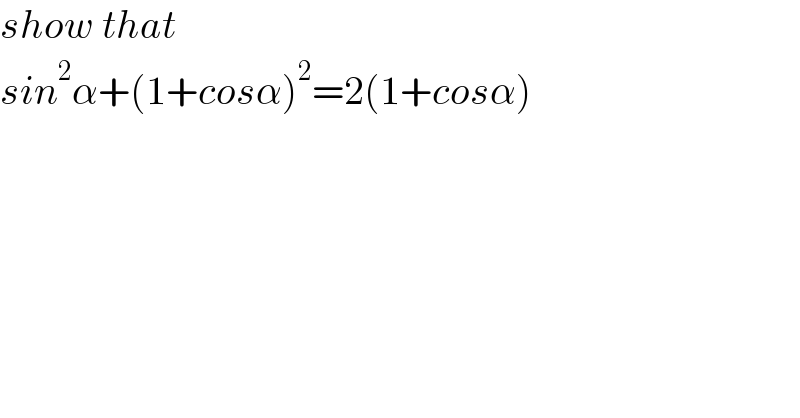
$${show}\:{that} \\ $$$${sin}^{\mathrm{2}} \alpha+\left(\mathrm{1}+{cos}\alpha\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}+{cos}\alpha\right) \\ $$
Answered by puissant last updated on 23/Jun/22
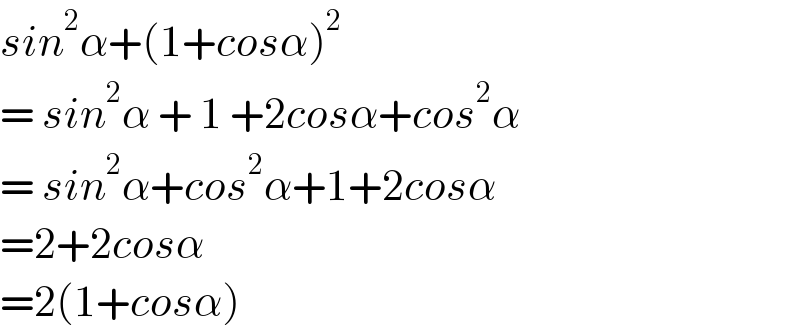
$${sin}^{\mathrm{2}} \alpha+\left(\mathrm{1}+{cos}\alpha\right)^{\mathrm{2}} \\ $$$$=\:{sin}^{\mathrm{2}} \alpha\:+\:\mathrm{1}\:+\mathrm{2}{cos}\alpha+{cos}^{\mathrm{2}} \alpha \\ $$$$=\:{sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha+\mathrm{1}+\mathrm{2}{cos}\alpha \\ $$$$=\mathrm{2}+\mathrm{2}{cos}\alpha \\ $$$$=\mathrm{2}\left(\mathrm{1}+{cos}\alpha\right) \\ $$
