Question Number 115765 by aye48 last updated on 28/Sep/20
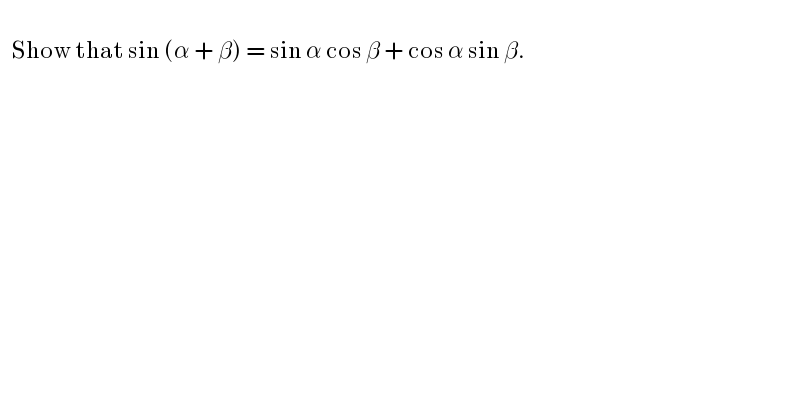
$$\: \\ $$$$\:\:\:\mathrm{Show}\:\mathrm{that}\:\mathrm{sin}\:\left(\alpha\:+\:\beta\right)\:=\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta\:+\:\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta. \\ $$
Commented by bemath last updated on 28/Sep/20
Commented by aye48 last updated on 28/Sep/20

$$\mathrm{Tk}\:\mathrm{yu}\:\mathrm{sir},\:\mathrm{explain}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step}\:\mathrm{pl}. \\ $$
Commented by Ar Brandon last updated on 28/Sep/20
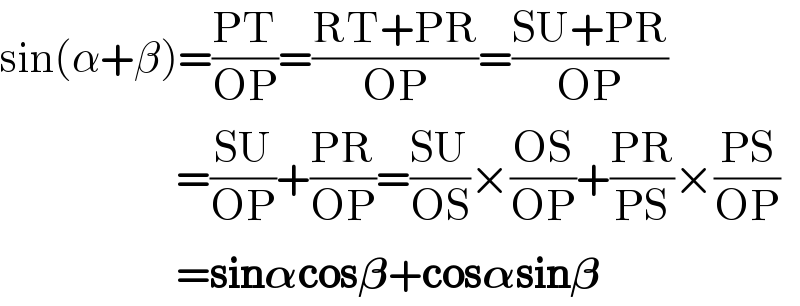
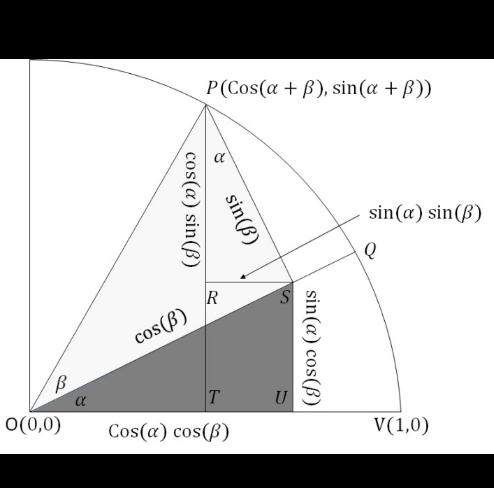
$$\mathrm{sin}\left(\alpha+\beta\right)=\frac{\mathrm{PT}}{\mathrm{OP}}=\frac{\mathrm{RT}+\mathrm{PR}}{\mathrm{OP}}=\frac{\mathrm{SU}+\mathrm{PR}}{\mathrm{OP}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{SU}}{\mathrm{OP}}+\frac{\mathrm{PR}}{\mathrm{OP}}=\frac{\mathrm{SU}}{\mathrm{OS}}×\frac{\mathrm{OS}}{\mathrm{OP}}+\frac{\mathrm{PR}}{\mathrm{PS}}×\frac{\mathrm{PS}}{\mathrm{OP}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{sin}\alpha\mathrm{cos}\beta}+\boldsymbol{\mathrm{cos}\alpha\mathrm{sin}\beta} \\ $$
Answered by MJS_new last updated on 28/Sep/20
![remember sin x =((e^(ix) −e^(−ix) )/(2i))=−(i/2)(e^(ix) −(1/e^(ix) )) cos x =((e^(ux) +e^(−ix) )/2) ⇒ sin (α+β) =−(i/2)(e^(iα) e^(iβ) −(1/(e^(iα) e^(iβ) )))= [let e^(iα) =p∧e^(iβ) =q] =−(i/2)(pq−(1/(pq)))= [now the trick:] =−(i/4)(2pq−(2/(pq)))= =−(i/4)(2pq−(2/(pq))+((p/q)+(q/p))−((p/q)+(q/p)))= =−(i/4)((pq+(p/q)−(q/p)−(1/(pq)))+(pq−(p/q)+(q/p)−(1/(pq))))= =−(i/4)((p−(1/p))(q+(1/q))+(p+(1/p))(q−(1/q)))= =−((i(p−(1/p)))/2)×((q+(1/q))/2)−((p+(1/p))/2)×((i(q−(1/q)))/2)= =((e^(iα) −e^(−iα) )/(2i))×((e^(iβ) +e^(−iβ) )/2)+((e^(iα) +e^(−iα) )/2)×((e^(iβ) −e^(−iβ) )/(2i))= =sin α cos β +cos α sin β](https://www.tinkutara.com/question/Q115767.png)
$$\mathrm{remember} \\ $$$$\mathrm{sin}\:{x}\:=\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2i}}=−\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{e}^{\mathrm{i}{x}} −\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{i}{x}} }\right) \\ $$$$\mathrm{cos}\:{x}\:=\frac{\mathrm{e}^{\mathrm{u}{x}} +\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}\:\left(\alpha+\beta\right)\:=−\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{e}^{\mathrm{i}\alpha} \mathrm{e}^{\mathrm{i}\beta} −\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{i}\alpha} \mathrm{e}^{\mathrm{i}\beta} }\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{let}\:\mathrm{e}^{\mathrm{i}\alpha} ={p}\wedge\mathrm{e}^{\mathrm{i}\beta} ={q}\right] \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\left({pq}−\frac{\mathrm{1}}{{pq}}\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{now}\:\mathrm{the}\:\mathrm{trick}:\right] \\ $$$$=−\frac{\mathrm{i}}{\mathrm{4}}\left(\mathrm{2}{pq}−\frac{\mathrm{2}}{{pq}}\right)= \\ $$$$=−\frac{\mathrm{i}}{\mathrm{4}}\left(\mathrm{2}{pq}−\frac{\mathrm{2}}{{pq}}+\left(\frac{{p}}{{q}}+\frac{{q}}{{p}}\right)−\left(\frac{{p}}{{q}}+\frac{{q}}{{p}}\right)\right)= \\ $$$$=−\frac{\mathrm{i}}{\mathrm{4}}\left(\left({pq}+\frac{{p}}{{q}}−\frac{{q}}{{p}}−\frac{\mathrm{1}}{{pq}}\right)+\left({pq}−\frac{{p}}{{q}}+\frac{{q}}{{p}}−\frac{\mathrm{1}}{{pq}}\right)\right)= \\ $$$$=−\frac{\mathrm{i}}{\mathrm{4}}\left(\left({p}−\frac{\mathrm{1}}{{p}}\right)\left({q}+\frac{\mathrm{1}}{{q}}\right)+\left({p}+\frac{\mathrm{1}}{{p}}\right)\left({q}−\frac{\mathrm{1}}{{q}}\right)\right)= \\ $$$$=−\frac{\mathrm{i}\left({p}−\frac{\mathrm{1}}{{p}}\right)}{\mathrm{2}}×\frac{{q}+\frac{\mathrm{1}}{{q}}}{\mathrm{2}}−\frac{{p}+\frac{\mathrm{1}}{{p}}}{\mathrm{2}}×\frac{\mathrm{i}\left({q}−\frac{\mathrm{1}}{{q}}\right)}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{e}^{\mathrm{i}\alpha} −\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2i}}×\frac{\mathrm{e}^{\mathrm{i}\beta} +\mathrm{e}^{−\mathrm{i}\beta} }{\mathrm{2}}+\frac{\mathrm{e}^{\mathrm{i}\alpha} +\mathrm{e}^{−\mathrm{i}\alpha} }{\mathrm{2}}×\frac{\mathrm{e}^{\mathrm{i}\beta} −\mathrm{e}^{−\mathrm{i}\beta} }{\mathrm{2i}}= \\ $$$$=\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta\:+\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta \\ $$
Commented by Dwaipayan Shikari last updated on 28/Sep/20
$$\mathrm{Great}\:\mathrm{thinking}\:\mathrm{sir}! \\ $$
