Question Number 95562 by peter frank last updated on 26/May/20
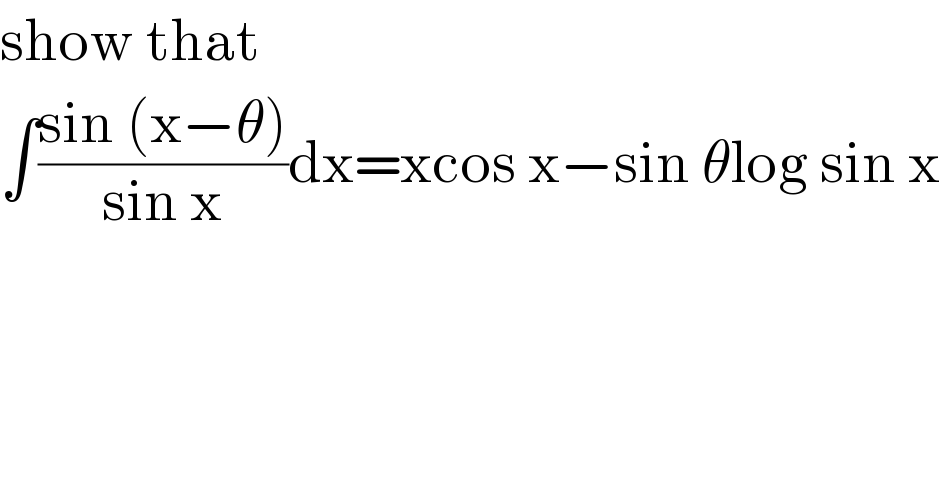
$$\mathrm{show}\:\mathrm{that} \\ $$$$\int\frac{\mathrm{sin}\:\left(\mathrm{x}−\theta\right)}{\mathrm{sin}\:\mathrm{x}}\mathrm{dx}=\mathrm{xcos}\:\mathrm{x}−\mathrm{sin}\:\theta\mathrm{log}\:\mathrm{sin}\:\mathrm{x} \\ $$
Answered by Ar Brandon last updated on 26/May/20
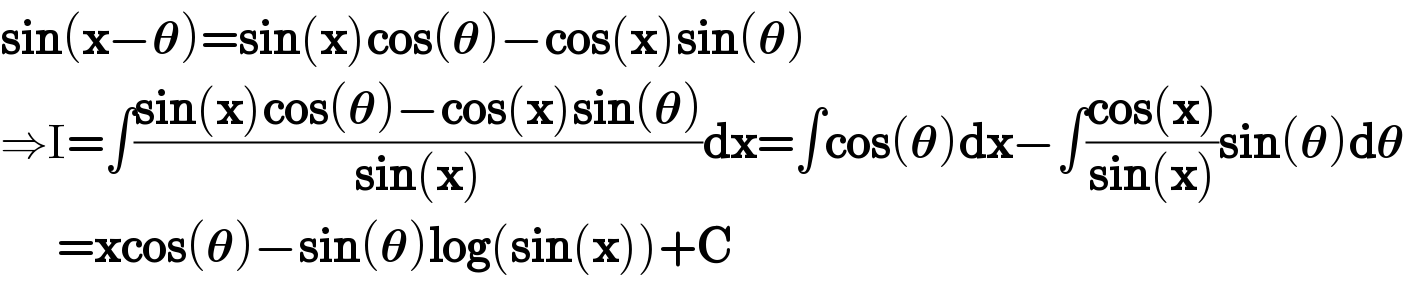
$$\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\theta}\right)=\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\theta}\right)−\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\theta}\right) \\ $$$$\Rightarrow\mathrm{I}=\int\frac{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\theta}\right)−\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\theta}\right)}{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}\boldsymbol{\mathrm{dx}}=\int\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\theta}\right)\boldsymbol{\mathrm{dx}}−\int\frac{\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)}\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\theta}\right)\boldsymbol{\mathrm{d}\theta} \\ $$$$\:\:\:\:\:\:\:=\boldsymbol{\mathrm{xcos}}\left(\boldsymbol{\theta}\right)−\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\theta}\right)\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right)\right)+\boldsymbol{\mathrm{C}} \\ $$
