Question Number 37663 by Rio Mike last updated on 16/Jun/18
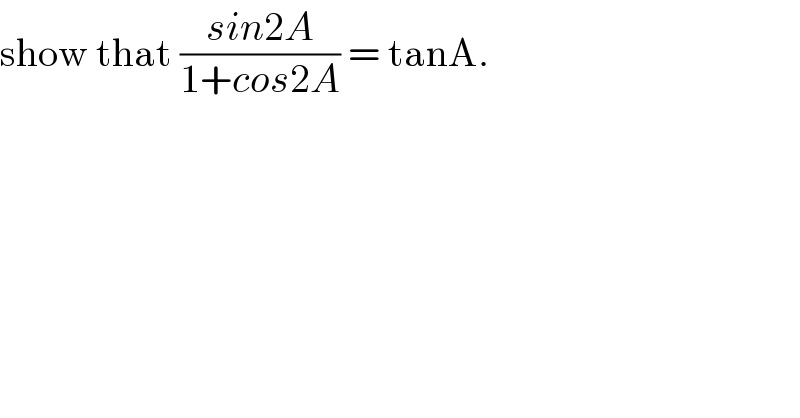
$$\mathrm{show}\:\mathrm{that}\:\frac{{sin}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}\:=\:\mathrm{tanA}. \\ $$
Answered by Joel579 last updated on 16/Jun/18
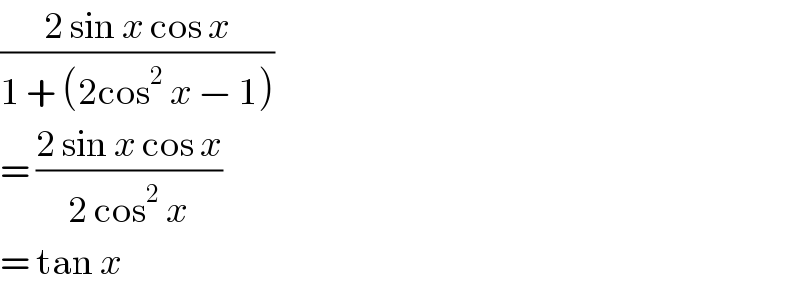
$$\frac{\mathrm{2}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{1}\:+\:\left(\mathrm{2cos}^{\mathrm{2}} \:{x}\:−\:\mathrm{1}\right)} \\ $$$$=\:\frac{\mathrm{2}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$=\:\mathrm{tan}\:{x} \\ $$
Answered by kunal1234523 last updated on 16/Jun/18
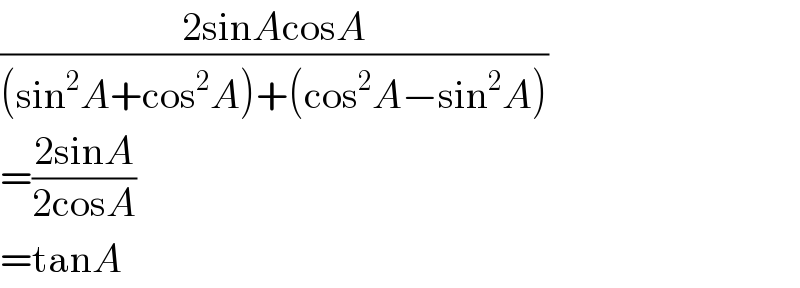
$$\frac{\mathrm{2sin}{A}\mathrm{cos}{A}}{\left(\mathrm{sin}^{\mathrm{2}} {A}+\mathrm{cos}^{\mathrm{2}} {A}\right)+\left(\mathrm{cos}^{\mathrm{2}} {A}−\mathrm{sin}^{\mathrm{2}} {A}\right)} \\ $$$$=\frac{\mathrm{2sin}{A}}{\mathrm{2cos}{A}} \\ $$$$=\mathrm{tan}{A}\:\: \\ $$
Answered by Ahmed Neutron last updated on 17/Jun/18

$$\frac{\mathrm{2sin}{A}.\mathrm{cos}{A}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} {A}−\mathrm{sin}^{\mathrm{2}} {A}} \\ $$$$\frac{\mathrm{2sin}{A}.\mathrm{cos}{A}}{\mathrm{sin}^{\mathrm{2}} {A}+\mathrm{cos}^{\mathrm{2}} {A}+\mathrm{cos}^{\mathrm{2}} {A}−\mathrm{sin}^{\mathrm{2}} {A}} \\ $$$$\frac{\mathrm{2sin}{A}.\mathrm{cos}{A}}{\mathrm{2cos}^{\mathrm{2}} {A}}=\frac{\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}=\mathrm{tan}{A} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
