Question Number 38011 by Rio Mike last updated on 20/Jun/18
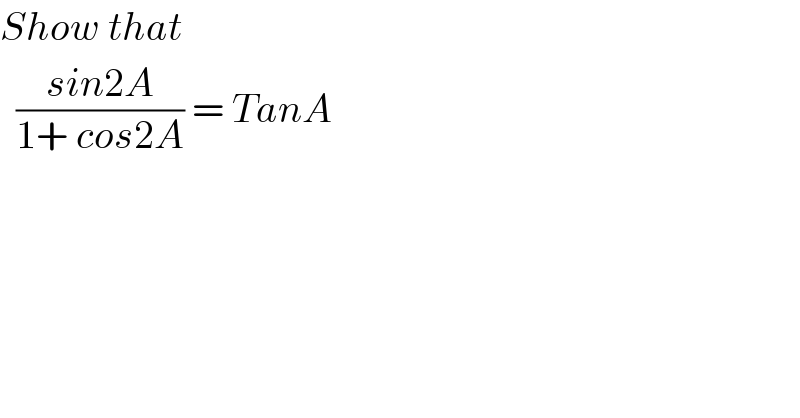
$${Show}\:{that}\: \\ $$$$\:\:\frac{{sin}\mathrm{2}{A}}{\mathrm{1}+\:{cos}\mathrm{2}{A}}\:=\:{TanA} \\ $$
Answered by MJS last updated on 20/Jun/18
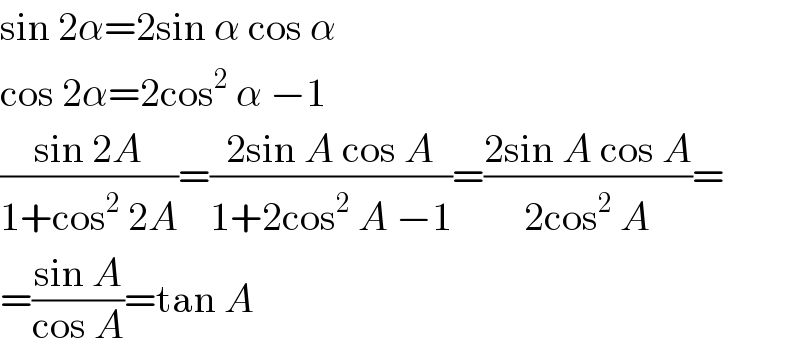
$$\mathrm{sin}\:\mathrm{2}\alpha=\mathrm{2sin}\:\alpha\:\mathrm{cos}\:\alpha \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\mathrm{2cos}^{\mathrm{2}} \:\alpha\:−\mathrm{1} \\ $$$$\frac{\mathrm{sin}\:\mathrm{2}{A}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{A}}=\frac{\mathrm{2sin}\:{A}\:\mathrm{cos}\:{A}}{\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{A}\:−\mathrm{1}}=\frac{\mathrm{2sin}\:{A}\:\mathrm{cos}\:{A}}{\mathrm{2cos}^{\mathrm{2}} \:{A}}= \\ $$$$=\frac{\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}=\mathrm{tan}\:{A} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jun/18
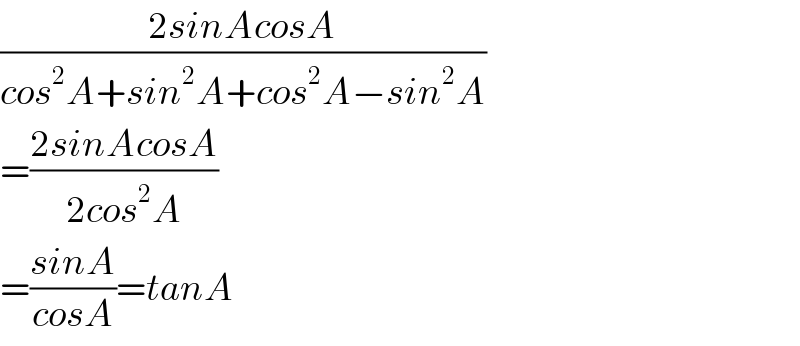
$$\frac{\mathrm{2}{sinAcosA}}{{cos}^{\mathrm{2}} {A}+{sin}^{\mathrm{2}} {A}+{cos}^{\mathrm{2}} {A}−{sin}^{\mathrm{2}} {A}} \\ $$$$=\frac{\mathrm{2}{sinAcosA}}{\mathrm{2}{cos}^{\mathrm{2}} {A}} \\ $$$$=\frac{{sinA}}{{cosA}}={tanA} \\ $$
