Menu Close

show-that-tan-1-x-ln-x-2-2ix-1-ln-x-2-1-2i-

Tinku Tara 0 Comments
Pin




Question Number 86550 by DuDono last updated on 29/Mar/20
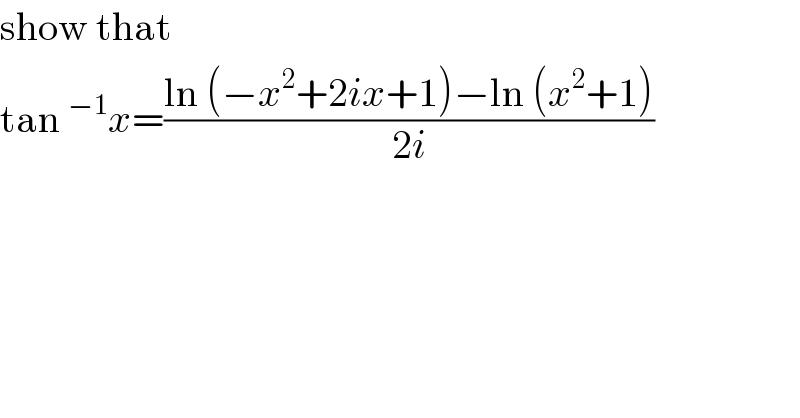
show that tan^(−1) x=((ln (−x^2 +2ix+1)−ln (x^2 +1))/(2i))
$$\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{tan}\:^{−\mathrm{1}} {x}=\frac{\mathrm{ln}\:\left(−{x}^{\mathrm{2}} +\mathrm{2}{ix}+\mathrm{1}\right)−\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}{i}} \\ $$
Commented by john santu last updated on 29/Mar/20
y = tan x = ((sin x)/(cos x)) y = ((e^(ix) −e^(−ix) )/(2i)) × ((2i)/(e^(ix) +e^(−ix) )) y = ((e^(ix) −e^(−ix) )/(e^(ix) +e^(−ix) )) ⇒ ye^(ix) +ye^(−ix) = e^(ix) −e^(−ix) (y+1)e^(−ix) = e^(ix) (1−y) [ e^(ix) = w ] ((y+1)/w) = w (1−y) ⇒ w^2 (1−y)−(1+y) =0 w = ± (√((y+1)/(y−1))) you can solve it
$$\mathrm{y}\:=\:\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}} \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}\:×\:\frac{\mathrm{2i}}{\mathrm{e}^{\mathrm{ix}} +\mathrm{e}^{−\mathrm{ix}} } \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{e}^{\mathrm{ix}} +\mathrm{e}^{−\mathrm{ix}} }\:\Rightarrow\:\mathrm{ye}^{\mathrm{ix}} +\mathrm{ye}^{−\mathrm{ix}} \:=\:\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} \\ $$$$\left(\mathrm{y}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{ix}} \:=\:\mathrm{e}^{\mathrm{ix}} \:\left(\mathrm{1}−\mathrm{y}\right)\:\left[\:\mathrm{e}^{\mathrm{ix}} \:=\:\mathrm{w}\:\right] \\ $$$$\frac{\mathrm{y}+\mathrm{1}}{\mathrm{w}}\:=\:\mathrm{w}\:\left(\mathrm{1}−\mathrm{y}\right)\:\Rightarrow\:\mathrm{w}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{y}\right)−\left(\mathrm{1}+\mathrm{y}\right)\:=\mathrm{0} \\ $$$$\mathrm{w}\:=\:\pm\:\sqrt{\frac{\mathrm{y}+\mathrm{1}}{\mathrm{y}−\mathrm{1}}} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it} \\ $$
Commented by Prithwish Sen 1 last updated on 29/Mar/20
RHS ((ln(((1+ix)^2 )/({1−(ix)^2 })))/(2i)) = ((ln(1+ix)−ln(1−ix))/(2i)) =(({ln(√(1+x^2 )) + i(2nπ+tan^(−1) x)}−{ln(√(1+x^2 )) +i(2nπ−tan^(−1) x)})/(2i)) = tan^(−1) x please check.
$$\mathrm{RHS} \\ $$$$\frac{\mathrm{ln}\frac{\left(\mathrm{1}+\mathrm{ix}\right)^{\mathrm{2}} }{\left\{\mathrm{1}−\left(\mathrm{ix}\right)^{\mathrm{2}} \right\}}}{\mathrm{2i}}\:=\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{ix}\right)−\mathrm{ln}\left(\mathrm{1}−\mathrm{ix}\right)}{\mathrm{2i}} \\ $$$$=\frac{\left\{\mathrm{ln}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{i}\left(\mathrm{2n}\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\right)\right\}−\left\{\mathrm{ln}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{i}\left(\mathrm{2n}\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\right)\right\}}{\mathrm{2i}} \\ $$$$=\:\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20
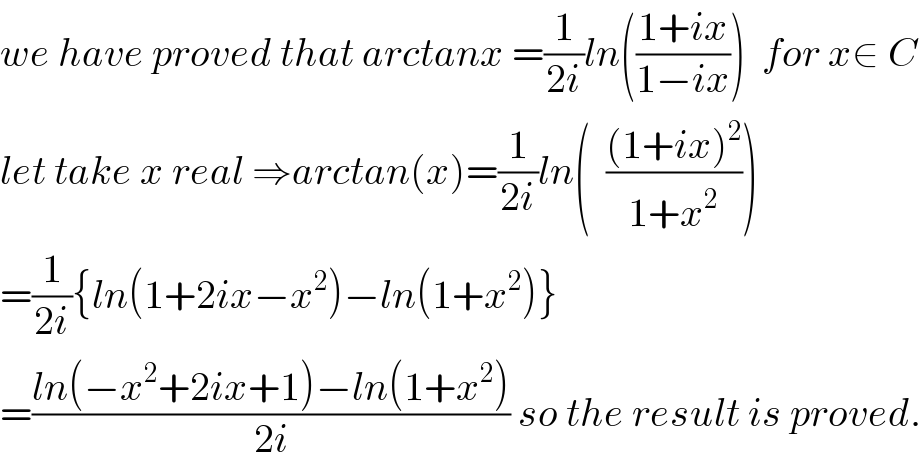
we have proved that arctanx =(1/(2i))ln(((1+ix)/(1−ix))) for x∈ C let take x real ⇒arctan(x)=(1/(2i))ln( (((1+ix)^2 )/(1+x^2 ))) =(1/(2i)){ln(1+2ix−x^2 )−ln(1+x^2 )} =((ln(−x^2 +2ix+1)−ln(1+x^2 ))/(2i)) so the result is proved.
$${we}\:{have}\:{proved}\:{that}\:{arctanx}\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{ix}}{\mathrm{1}−{ix}}\right)\:\:{for}\:{x}\in\:{C} \\ $$$${let}\:{take}\:{x}\:{real}\:\Rightarrow{arctan}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\:\:\frac{\left(\mathrm{1}+{ix}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{{ln}\left(\mathrm{1}+\mathrm{2}{ix}−{x}^{\mathrm{2}} \right)−{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right\} \\ $$$$=\frac{{ln}\left(−{x}^{\mathrm{2}} +\mathrm{2}{ix}+\mathrm{1}\right)−{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{2}{i}}\:{so}\:{the}\:{result}\:{is}\:{proved}. \\ $$
Answered by Ar Brandon last updated on 30/Mar/20

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *