Question Number 58312 by pete last updated on 21/Apr/19

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{angle}\:\theta\:\mathrm{between}\:\mathrm{two}\:\mathrm{unit} \\ $$$$\mathrm{vectors}\:\underset{�} {\hat {\mathrm{a}}}\:\mathrm{and}\:\underset{�} {\hat {\mathrm{b}}}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}\:\mathrm{cos}\theta=\underset{�} {\hat {\mathrm{a}}}\bullet\underset{�} {\hat {\mathrm{b}}}. \\ $$$$\mathrm{Hence},\:\mathrm{given}\:\mathrm{that}\:\underset{�} {\hat {\mathrm{a}}}=\underset{�} {\mathrm{i}cosA}+\underset{�} {\mathrm{j}sinA}\:\mathrm{and} \\ $$$$\underset{�} {\hat {\mathrm{b}}}=\underset{�} {\mathrm{i}cosB}−\underset{�} {\mathrm{j}sinB},\:\mathrm{prove}\:\mathrm{that}\:\mathrm{cos}\left(\mathrm{A}+\mathrm{B}\right)= \\ $$$$\mathrm{cosAcosB}−\mathrm{sinAsinB}. \\ $$
Commented by tanmay last updated on 21/Apr/19
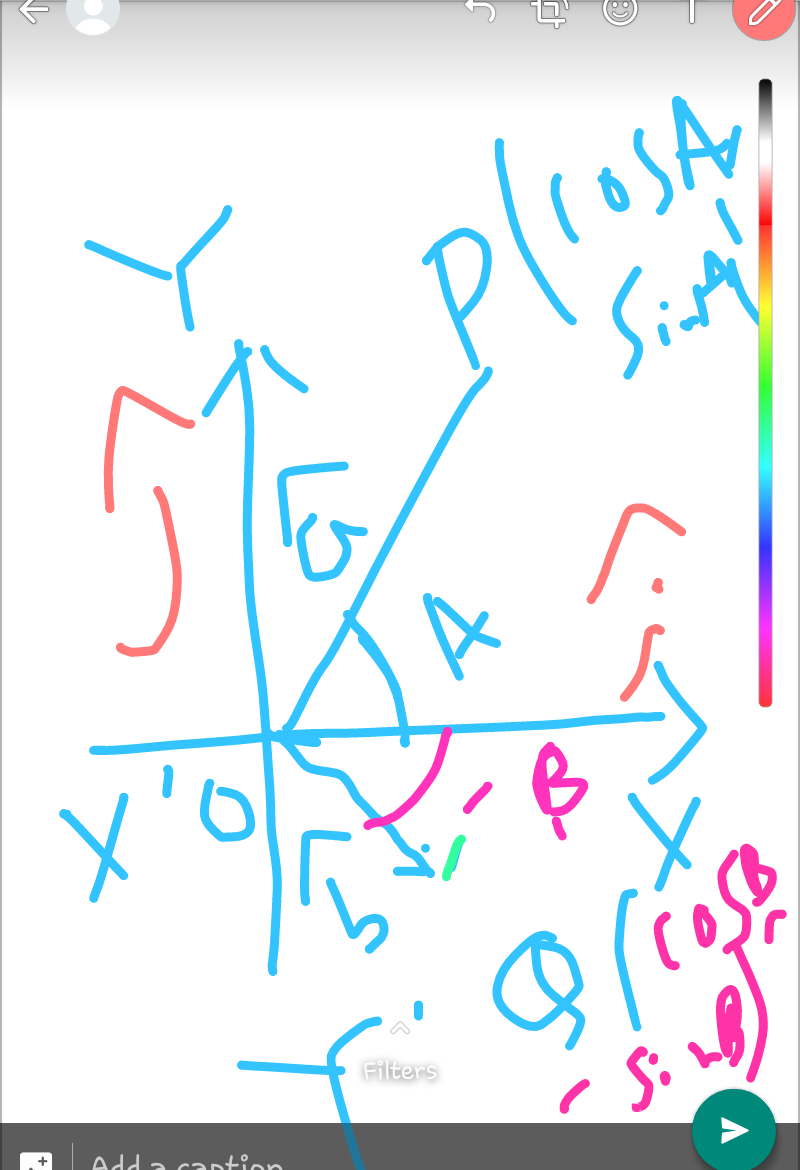
Commented by tanmay last updated on 21/Apr/19

$${vector}\:{o}\overset{\rightarrow} {{p}}=\overset{\wedge} {{a}}={icosA}+{jsinA} \\ $$$${vector}\:{o}\overset{\rightarrow} {{Q}}=\overset{\wedge} {{b}}={icosB}−{jsinB} \\ $$$${angle}\:{between}\:{o}\overset{\rightarrow} {{p}}\:{and}\:{o}\overset{\rightarrow} {{Q}}\:{is}<{POQ}={A}+{B} \\ $$$$\overset{\wedge} {{a}}.\overset{\wedge} {{b}}=\mid\overset{\wedge} {{a}}\mid\:\mid\overset{\wedge} {{b}}\mid\:{cos}\left({A}+{B}\right)=\mathrm{1}×\mathrm{1}×{cos}\left({A}+{B}\right)={cos}\left({A}+{B}\right) \\ $$$$\overset{\wedge} {{a}}.\overset{\wedge} {{b}} \\ $$$$=\left({icosA}+{jsinA}\right).\left({icosB}−{jsinB}\right) \\ $$$$={cosAcosB}−{sinA}\:{sinB} \\ $$$${hence}\:{equating}\:{value}\:{of}\:\overset{\wedge} {{a}}.\overset{\wedge} {{b}} \\ $$$${cos}\left({A}+{B}\right)={cosAcosB}−{sinB} \\ $$$${formula}… \\ $$$${if}\:\overset{\rightarrow} {{A}}={ix}_{\mathrm{1}} +{jy}_{\mathrm{1}} +{kz}_{\mathrm{1}} \\ $$$$\overset{\rightarrow} {{B}}={ix}_{\mathrm{2}} +{jy}_{\mathrm{2}} +{kz}_{\mathrm{2}} \\ $$$$\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}=\mid\overset{\rightarrow} {{A}}\mid\:\mid\overset{\rightarrow} {{B}}\mid\:\:{cos}\theta \\ $$$$\mid{A}\mid=\sqrt{{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{1}} ^{\mathrm{2}} }\:\:\:{and}\:\mid\overset{\rightarrow} {{B}}\mid=\sqrt{{x}_{\mathrm{2}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} +{z}_{\mathrm{2}} ^{\mathrm{2}} }\: \\ $$$$\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}={x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} +{z}_{\mathrm{1}} {z}_{\mathrm{2}} \\ $$$${cos}\theta=\frac{\overset{\rightarrow} {{A}}.\overset{\rightarrow} {{B}}}{\mid\overset{\rightarrow} {{A}}\mid\:\mid\overset{\rightarrow} {{B}}\mid}=\frac{{x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} +{z}_{\mathrm{1}} {z}_{\mathrm{2}} }{\:\sqrt{{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{1}} ^{\mathrm{2}} }\:\:×\sqrt{{x}_{\mathrm{2}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} +{z}_{\mathrm{2}} ^{\mathrm{2}} }\:} \\ $$$$ \\ $$
Commented by pete last updated on 21/Apr/19
$$\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much} \\ $$
Commented by tanmay last updated on 21/Apr/19

$${most}\:{welcome}… \\ $$
