Menu Close

show-that-the-common-chord-of-the-circle-x-2-y-2-4-and-x-2-y-2-4x-2y-4-0-passes-through-the-origin-

Tinku Tara 0 Comments
Pin




Question Number 171164 by MathsFan last updated on 08/Jun/22
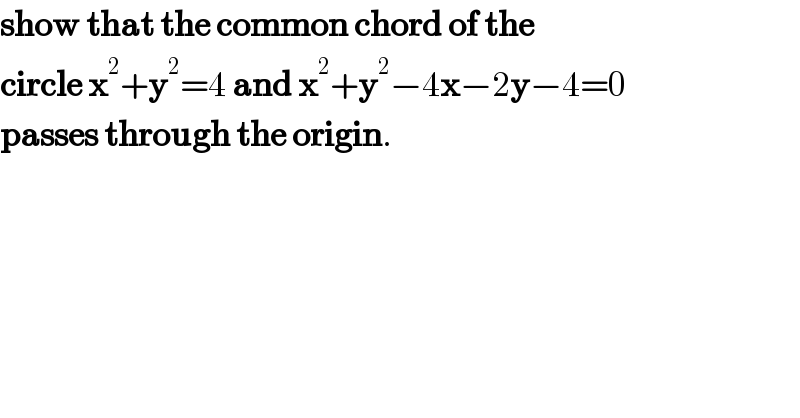
show that the common chord of the circle x^2 +y^2 =4 and x^2 +y^2 −4x−2y−4=0 passes through the origin.
showthatthecommonchordofthecirclex2+y2=4andx2+y2−4x−2y−4=0passesthroughtheorigin.
Answered by thfchristopher last updated on 09/Jun/22
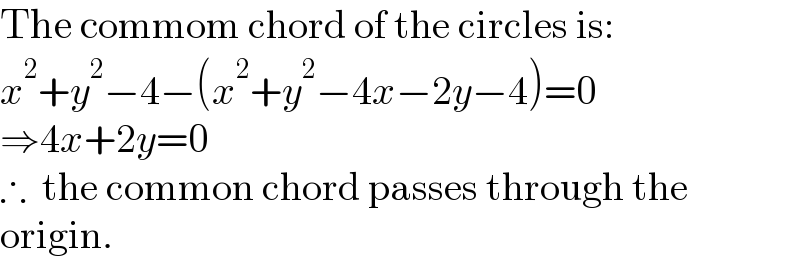
The commom chord of the circles is: x^2 +y^2 −4−(x^2 +y^2 −4x−2y−4)=0 ⇒4x+2y=0 ∴ the common chord passes through the origin.
Thecommomchordofthecirclesis:x2+y2−4−(x2+y2−4x−2y−4)=0⇒4x+2y=0∴thecommonchordpassesthroughtheorigin.
Commented by MathsFan last updated on 09/Jun/22
thanks
thanks
Answered by som(math1967) last updated on 09/Jun/22
x^2 +y^2 =4 g_1 =0,f_1 =0,c_1 =−4 x^2 +y^2 −4x−2y−4=0 g_2 =−2 ,f_2 =−1,c_2 =−4 equation of common chord (0+2)x+(0+1)y+(−4+4)=0 ⇒2x+y=0 ∴ passes origin (ax+by=0 form) Other way c_1 −c_2 =−4+4=0 ∴ common chord passes origin
x2+y2=4g1=0,f1=0,c1=−4x2+y2−4x−2y−4=0g2=−2,f2=−1,c2=−4equationofcommonchord(0+2)x+(0+1)y+(−4+4)=0⇒2x+y=0∴passesorigin(ax+by=0form)Otherwayc1−c2=−4+4=0∴commonchordpassesorigin
Commented by MathsFan last updated on 09/Jun/22
thank you
thankyou

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *