Question Number 169364 by Mastermind last updated on 29/Apr/22
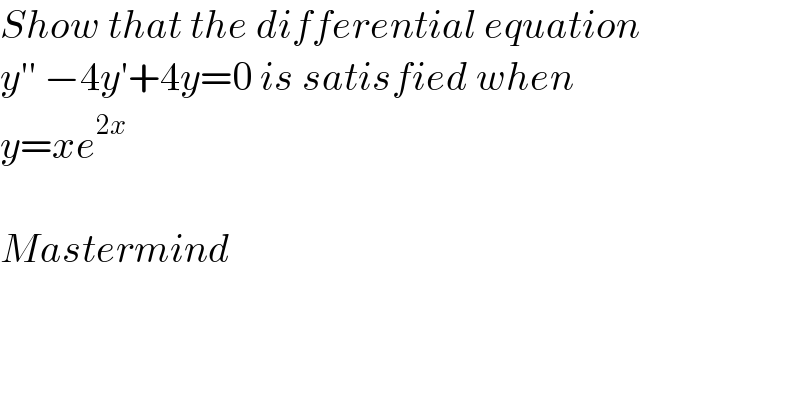
$${Show}\:{that}\:{the}\:{differential}\:{equation} \\ $$$${y}''\:−\mathrm{4}{y}'+\mathrm{4}{y}=\mathrm{0}\:{is}\:{satisfied}\:{when} \\ $$$${y}={xe}^{\mathrm{2}{x}} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by Mathspace last updated on 29/Apr/22
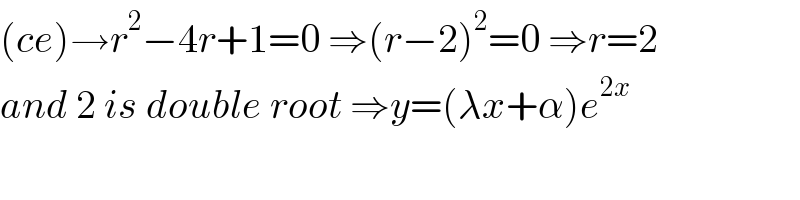
$$\left({ce}\right)\rightarrow{r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{1}=\mathrm{0}\:\Rightarrow\left({r}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow{r}=\mathrm{2} \\ $$$${and}\:\mathrm{2}\:{is}\:{double}\:{root}\:\Rightarrow{y}=\left(\lambda{x}+\alpha\right){e}^{\mathrm{2}{x}} \\ $$
