Question Number 41721 by Rio Michael last updated on 11/Aug/18
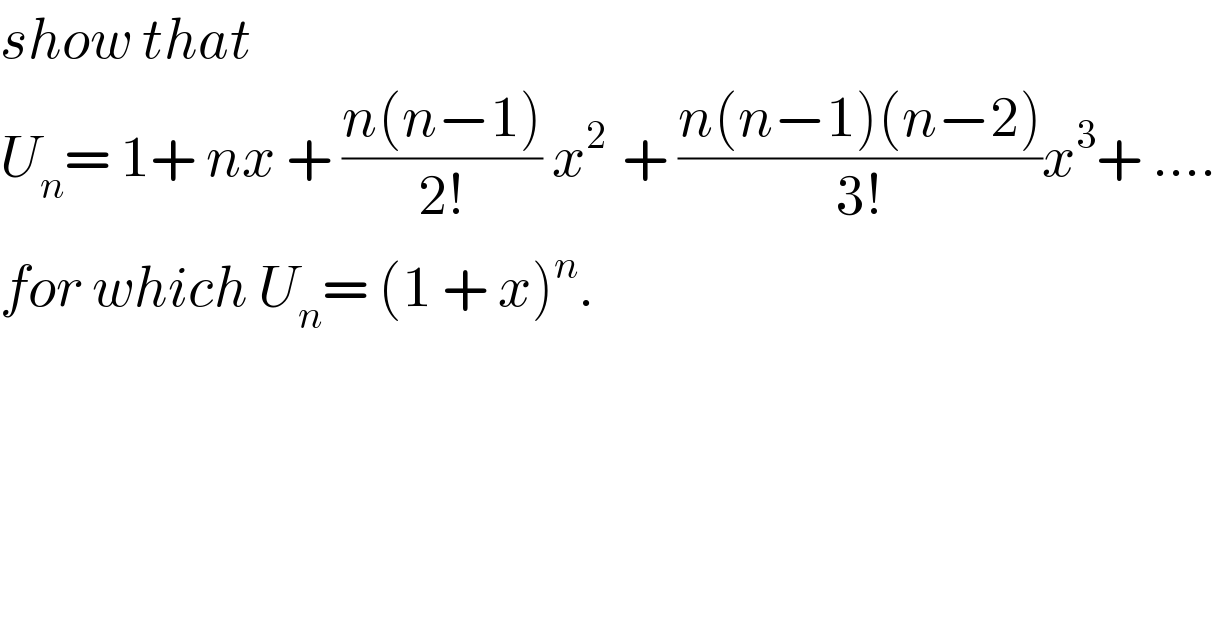
$${show}\:{that} \\ $$$${U}_{{n}} =\:\mathrm{1}+\:{nx}\:+\:\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}\:{x}^{\mathrm{2}\:\:} +\:\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +\:…. \\ $$$${for}\:{which}\:{U}_{{n}} =\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} . \\ $$
Commented by maxmathsup by imad last updated on 12/Aug/18

$${let}\:{p}\left({x}\right)\:=\left(\mathrm{1}+{x}\right)^{{n}} \:\:\:\:{we}\:{have}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{\infty} \:\:\frac{{p}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{x}^{{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{{p}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{x}^{{k}} \:+\sum_{{k}={n}+\mathrm{1}} ^{\infty} \:\:\frac{{p}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:\:{but}\:{for}\:{k}>{n}\:\:\:{p}^{\left({k}\right)} \left({x}\right)=\mathrm{0}\Rightarrow \\ $$$${p}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{{p}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}\:{x}^{{k}} \:\:\:{but}\:{binomial}\:{formulae}\:{give} \\ $$$${p}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:{x}^{{k}} \:\:=\:{C}_{{n}} ^{\mathrm{0}} \:\:+{C}_{{n}} ^{\mathrm{1}} \:{x}\:\:+\:{C}_{{n}} ^{{n}} \:{x}^{\mathrm{2}} \:+….+\:{C}_{{n}} ^{{n}} \:{x}^{{n}} \\ $$$$=\mathrm{1}+{nx}\:+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\:{x}^{\mathrm{2}} \:+…..+{x}^{{n}} \:\:\:\:\left({so}\:{the}\:{sum}\:{is}\:{not}\:{infinite}\right) \\ $$
