Menu Close

Show-that-x-2-2xy-3y-2-1-is-a-solution-to-the-differential-equation-x-3y-2-d-2-y-dx-2-2-x-2-2xy-2y-3-0-

Tinku Tara 0 Comments
Pin




Question Number 173736 by Tawa11 last updated on 17/Jul/22
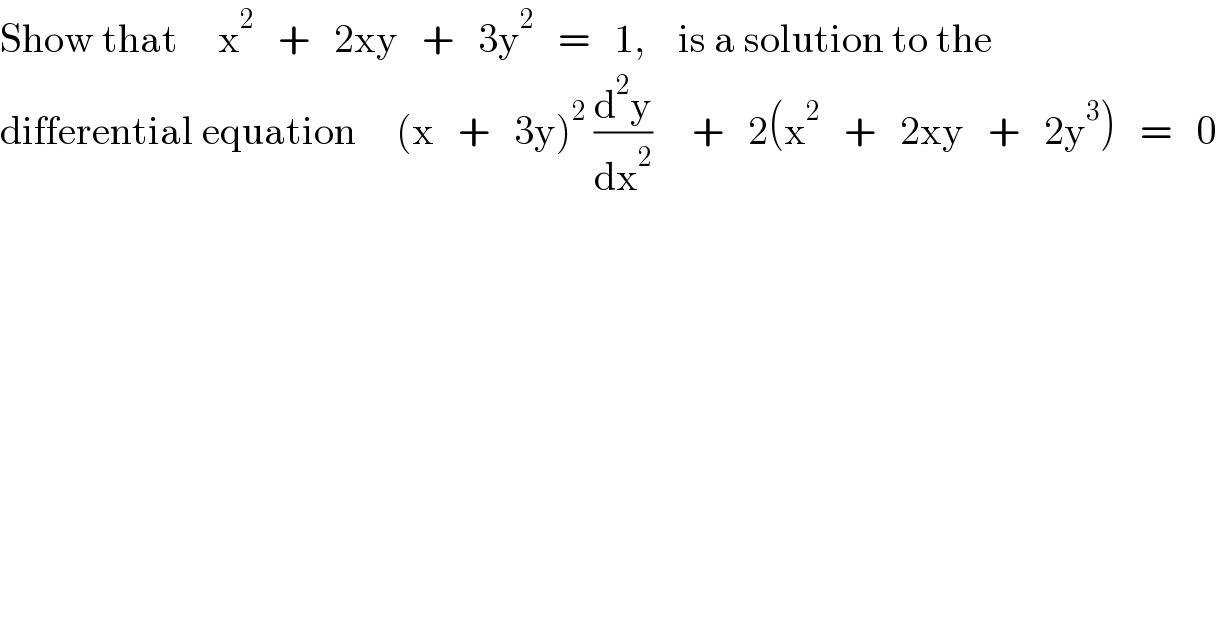
Show that x^2 + 2xy + 3y^2 = 1, is a solution to the differential equation (x + 3y)^2 (d^2 y/dx^2 ) + 2(x^2 + 2xy + 2y^3 ) = 0
$$\mathrm{Show}\:\mathrm{that}\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:\:+\:\:\:\mathrm{2xy}\:\:\:+\:\:\:\mathrm{3y}^{\mathrm{2}} \:\:\:=\:\:\:\mathrm{1},\:\:\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{differential}\:\mathrm{equation}\:\:\:\:\:\left(\mathrm{x}\:\:\:+\:\:\:\mathrm{3y}\right)^{\mathrm{2}} \:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:\:\:\:\:+\:\:\:\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \:\:\:+\:\:\:\mathrm{2xy}\:\:\:+\:\:\:\mathrm{2y}^{\mathrm{3}} \right)\:\:\:=\:\:\:\mathrm{0} \\ $$
Answered by mindispower last updated on 17/Jul/22
(d/dx)(x^2 +2xy+3y^2 )=0 ⇔(2x+2y+2x(dy/dx)+((6dy)/dx)y)=0 (d/dx)(2x+2y+2x(dy/dx)+((6dy)/dx)y)=0 ⇎2+((2dy)/dx)+2(dy/dx)+2x(d^2 y/dx^2 )+((6d^2 y)/dx^2 )y+6((dy/dx))^2 =0 (dy/dx)=((−2x−2y)/(2x+6y)) (d^2 y/dx^2 )=(1/(2x+6y))(−2+((8x+8y)/(2x+6y))−6(((2x+2y)/(2x+6y)))^2 ) (x+3y)^3 (d^2 y/dx^2 )=(1/2)(x+3y)^2 (−2+((4x+4y)/(x+3y))−6(((x+y)/(x+3y)))^2_) =−3(x+y)^2 −(x+3y)^2 +(2x+2y)(x+3y) −2x^2 −6y^2 −4xy ⇒(x+3y)^2 (d^2 y/dx^2 )+2(x^2 +2xy+3y^2 )=0 May bee i have mistak sorry sir
$$\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{3}{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{x}\frac{{dy}}{{dx}}+\frac{\mathrm{6}{dy}}{{dx}}{y}\right)=\mathrm{0} \\ $$$$\frac{{d}}{{dx}}\left(\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{x}\frac{{dy}}{{dx}}+\frac{\mathrm{6}{dy}}{{dx}}{y}\right)=\mathrm{0} \\ $$$$\nLeftrightarrow\mathrm{2}+\frac{\mathrm{2}{dy}}{{dx}}+\mathrm{2}\frac{{dy}}{{dx}}+\mathrm{2}{x}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\frac{\mathrm{6}{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }{y}+\mathrm{6}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{−\mathrm{2}{x}−\mathrm{2}{y}}{\mathrm{2}{x}+\mathrm{6}{y}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{6}{y}}\left(−\mathrm{2}+\frac{\mathrm{8}{x}+\mathrm{8}{y}}{\mathrm{2}{x}+\mathrm{6}{y}}−\mathrm{6}\left(\frac{\mathrm{2}{x}+\mathrm{2}{y}}{\mathrm{2}{x}+\mathrm{6}{y}}\right)^{\mathrm{2}} \right) \\ $$$$\left({x}+\mathrm{3}{y}\right)^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{3}{y}\right)^{\mathrm{2}} \left(−\mathrm{2}+\frac{\mathrm{4}{x}+\mathrm{4}{y}}{{x}+\mathrm{3}{y}}−\mathrm{6}\left(\frac{{x}+{y}}{{x}+\mathrm{3}{y}}\right)^{\mathrm{2}_{\left.\right)} } \right. \\ $$$$=−\mathrm{3}\left({x}+{y}\right)^{\mathrm{2}} −\left({x}+\mathrm{3}{y}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}+\mathrm{2}{y}\right)\left({x}+\mathrm{3}{y}\right) \\ $$$$−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{6}{y}^{\mathrm{2}} −\mathrm{4}{xy} \\ $$$$\Rightarrow\left({x}+\mathrm{3}{y}\right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{3}{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${May}\:{bee}\:{i}\:{have}\:{mistak}\:{sorry}\:{sir} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 17/Jul/22
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 17/Jul/22
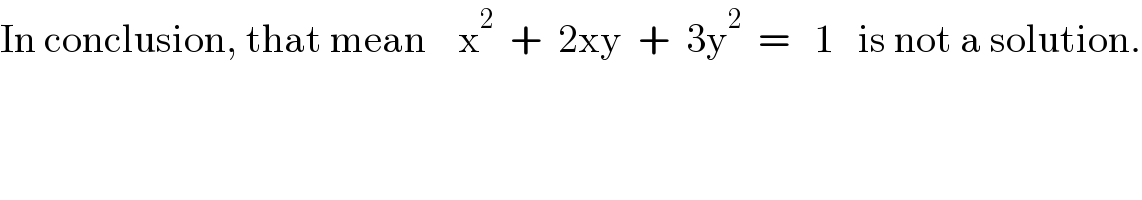
In conclusion, that mean x^2 + 2xy + 3y^2 = 1 is not a solution.
$$\mathrm{In}\:\mathrm{conclusion},\:\mathrm{that}\:\mathrm{mean}\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:+\:\:\mathrm{2xy}\:\:+\:\:\mathrm{3y}^{\mathrm{2}} \:\:=\:\:\:\mathrm{1}\:\:\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{solution}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *