Menu Close

show-that-x-y-x-y-

Tinku Tara 0 Comments
Pin




Question Number 119057 by mathocean1 last updated on 21/Oct/20
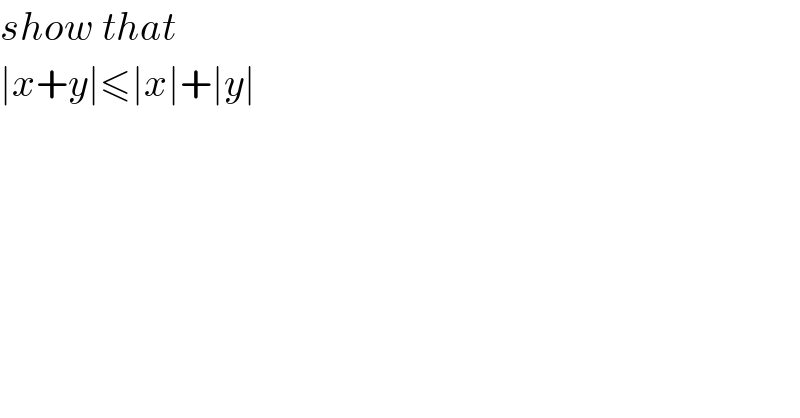
show that ∣x+y∣≤∣x∣+∣y∣
$${show}\:{that} \\ $$$$\mid{x}+{y}\mid\leqslant\mid{x}\mid+\mid{y}\mid \\ $$$$ \\ $$
Answered by Bird last updated on 21/Oct/20
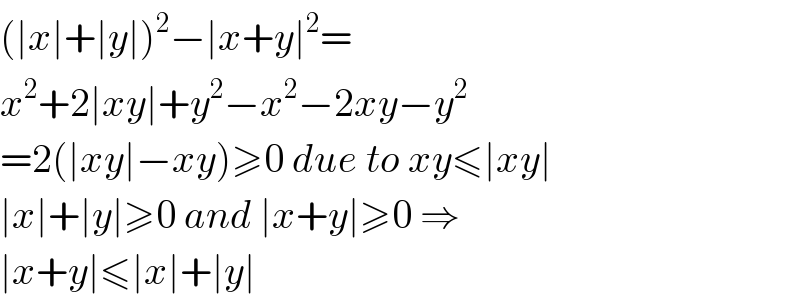
(∣x∣+∣y∣)^2 −∣x+y∣^2 = x^2 +2∣xy∣+y^2 −x^2 −2xy−y^2 =2(∣xy∣−xy)≥0 due to xy≤∣xy∣ ∣x∣+∣y∣≥0 and ∣x+y∣≥0 ⇒ ∣x+y∣≤∣x∣+∣y∣
$$\left(\mid{x}\mid+\mid{y}\mid\right)^{\mathrm{2}} −\mid{x}+{y}\mid^{\mathrm{2}} = \\ $$$${x}^{\mathrm{2}} +\mathrm{2}\mid{xy}\mid+{y}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{2}{xy}−{y}^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\mid{xy}\mid−{xy}\right)\geqslant\mathrm{0}\:{due}\:{to}\:{xy}\leqslant\mid{xy}\mid \\ $$$$\mid{x}\mid+\mid{y}\mid\geqslant\mathrm{0}\:{and}\:\mid{x}+{y}\mid\geqslant\mathrm{0}\:\Rightarrow \\ $$$$\mid{x}+{y}\mid\leqslant\mid{x}\mid+\mid{y}\mid \\ $$
Commented by mathocean1 last updated on 25/Oct/20
Thank you all sirs.
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{all}\:\mathrm{sirs}. \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 22/Oct/20
step 1. lemma: −∣x∣≤x≤∣x∣ proof: case 1. if x≥0 then x=∣x∣≤∣x∣ but also x≥0≥−∣x∣. case 2. if x≤0 then x≤0≤∣x∣ but x=−(−x)=−∣x∣≥−∣x∣ step 2. by lemma: −∣a∣≤a≤∣a∣ a≤∣a∣⇒a+b≤∣a∣+b≤∣a∣+∣b∣ a≥−∣a∣⇒a+b≥b−∣a∣≥−∣b∣−∣a∣ ⇒a+b≥−(∣a∣+∣b∣) ⇒−(∣a∣+∣b∣)≤a+b≤∣a∣+∣b∣ step 3. to show ∣a+b∣≤∣a∣+∣b∣ do by cases: case 1. a+b≥0 then ∣a+b∣=a+b≤∣a∣+∣b∣. case 2 a+b≤0 then ∣a+b∣=−(a+b)≤−(−(∣a∣+∣b∣))=∣a∣+∣b∣. Proved.
$$\mathrm{step}\:\mathrm{1}. \\ $$$$\mathrm{lemma}: \\ $$$$−\mid\mathrm{x}\mid\leqslant\mathrm{x}\leqslant\mid\mathrm{x}\mid \\ $$$$\mathrm{proof}: \\ $$$$\mathrm{case}\:\mathrm{1}. \\ $$$$\mathrm{if}\:\mathrm{x}\geqslant\mathrm{0}\:\mathrm{then}\:\mathrm{x}=\mid\mathrm{x}\mid\leqslant\mid\mathrm{x}\mid \\ $$$$\mathrm{but}\:\mathrm{also}\:\mathrm{x}\geqslant\mathrm{0}\geqslant−\mid\mathrm{x}\mid. \\ $$$$\mathrm{case}\:\mathrm{2}. \\ $$$$\mathrm{if}\:\mathrm{x}\leqslant\mathrm{0}\:\mathrm{then}\:\mathrm{x}\leqslant\mathrm{0}\leqslant\mid\mathrm{x}\mid \\ $$$$\mathrm{but}\:\mathrm{x}=−\left(−\mathrm{x}\right)=−\mid\mathrm{x}\mid\geqslant−\mid\mathrm{x}\mid \\ $$$$\mathrm{step}\:\mathrm{2}. \\ $$$$\mathrm{by}\:\mathrm{lemma}:\:−\mid\mathrm{a}\mid\leqslant\mathrm{a}\leqslant\mid\mathrm{a}\mid \\ $$$$\mathrm{a}\leqslant\mid\mathrm{a}\mid\Rightarrow\mathrm{a}+\mathrm{b}\leqslant\mid\mathrm{a}\mid+\mathrm{b}\leqslant\mid\mathrm{a}\mid+\mid\mathrm{b}\mid \\ $$$$\mathrm{a}\geqslant−\mid\mathrm{a}\mid\Rightarrow\mathrm{a}+\mathrm{b}\geqslant\mathrm{b}−\mid\mathrm{a}\mid\geqslant−\mid\mathrm{b}\mid−\mid\mathrm{a}\mid \\ $$$$\Rightarrow\mathrm{a}+\mathrm{b}\geqslant−\left(\mid\mathrm{a}\mid+\mid\mathrm{b}\mid\right) \\ $$$$\Rightarrow−\left(\mid\mathrm{a}\mid+\mid\mathrm{b}\mid\right)\leqslant\mathrm{a}+\mathrm{b}\leqslant\mid\mathrm{a}\mid+\mid\mathrm{b}\mid \\ $$$$\mathrm{step}\:\mathrm{3}. \\ $$$$\mathrm{to}\:\mathrm{show}\:\mid\mathrm{a}+\mathrm{b}\mid\leqslant\mid\mathrm{a}\mid+\mid\mathrm{b}\mid\:\mathrm{do}\:\mathrm{by}\:\mathrm{cases}: \\ $$$$\mathrm{case}\:\mathrm{1}. \\ $$$$\mathrm{a}+\mathrm{b}\geqslant\mathrm{0}\:\mathrm{then}\:\mid\mathrm{a}+\mathrm{b}\mid=\mathrm{a}+\mathrm{b}\leqslant\mid\mathrm{a}\mid+\mid\mathrm{b}\mid. \\ $$$$\mathrm{case}\:\mathrm{2} \\ $$$$\mathrm{a}+\mathrm{b}\leqslant\mathrm{0}\:\mathrm{then}\: \\ $$$$\mid\mathrm{a}+\mathrm{b}\mid=−\left(\mathrm{a}+\mathrm{b}\right)\leqslant−\left(−\left(\mid\mathrm{a}\mid+\mid\mathrm{b}\mid\right)\right)=\mid\mathrm{a}\mid+\mid\mathrm{b}\mid. \\ $$$$\mathrm{Proved}. \\ $$
Commented by mathocean1 last updated on 25/Oct/20
Thanks.
$$\mathrm{Thanks}. \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 22/Oct/20
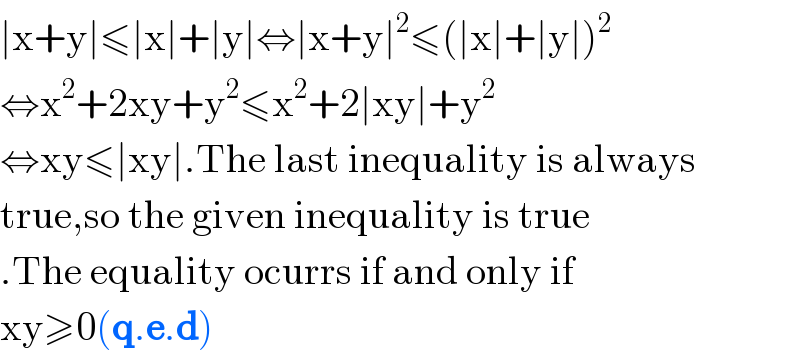
∣x+y∣≤∣x∣+∣y∣⇔∣x+y∣^2 ≤(∣x∣+∣y∣)^2 ⇔x^2 +2xy+y^2 ≤x^2 +2∣xy∣+y^2 ⇔xy≤∣xy∣.The last inequality is always true,so the given inequality is true .The equality ocurrs if and only if xy≥0(q.e.d)
$$\mid\mathrm{x}+\mathrm{y}\mid\leqslant\mid\mathrm{x}\mid+\mid\mathrm{y}\mid\Leftrightarrow\mid\mathrm{x}+\mathrm{y}\mid^{\mathrm{2}} \leqslant\left(\mid\mathrm{x}\mid+\mid\mathrm{y}\mid\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{x}^{\mathrm{2}} +\mathrm{2}\mid\mathrm{xy}\mid+\mathrm{y}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{xy}\leqslant\mid\mathrm{xy}\mid.\mathrm{The}\:\mathrm{last}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{always} \\ $$$$\mathrm{true},\mathrm{so}\:\mathrm{the}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true} \\ $$$$.\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\: \\ $$$$\mathrm{xy}\geqslant\mathrm{0}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right)\: \\ $$
Commented by mathocean1 last updated on 25/Oct/20
thanks.
$$\mathrm{thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *