Menu Close

similar-question-reposted-if-a-3-b-b-3-c-c-3-a-with-a-b-c-and-a-b-c-R-find-abc-2-

Tinku Tara 0 Comments
Pin




Question Number 161366 by mr W last updated on 17/Dec/21
[similar question reposted] if a+(3/b)=b+(3/c)=c+(3/a) with a≠b≠c and a,b,c ∈ R. find (abc)^2 =?
[similarquestionreposted]ifa+3b=b+3c=c+3awitha≠b≠canda,b,c∈R.find(abc)2=?
Answered by 1549442205PVT last updated on 18/Dec/21
From the hypothesis we have: a+(3/b)=c+(3/a)⇒c=((a^2 −3)/a)+(3/b)(1)⇒(3/c)=((3ab)/(a^2 b+3a−3b)) ⇒a+(3/b)=b+((3ab)/(a^2 b+3a−3b))⇒((ab+3−b^2 )/b)=((3ab)/(a^2 b+3a−3b)) ⇔a^3 b^2 +3a^2 b−a^2 b^3 +3a^2 b+9a−3ab^2 −3ab^2 −9b+3b^3 =3ab^2 After simplifycation we obtain a^3 b^2 −(b^3 −6b)a^2 −(9b^2 −9)a+3b^3 −9b =(a−b)(a^2 b^2 +6ab−3b^2 +9)=0.Since a≠b ,we get a^2 b^2 +6ab−3b^2 +9=0 ⇔(a^2 −3)b^2 +6ab+9=0. •if a^2 −3=0⇔a=±(√3) then b=((−3)/(±2(√3)))=((∓(√3))/2) ⇒c=∓2(√3)⇒abc=±3(√3) ⇒(abc)^2 =27 •if a^2 −3≠0.Then △′=9a^2 −9a^2 +27=27,so b=((−3a±3(√3))/(a^2 −3)).Hence from(1)weget bc=3+((a^2 −3)/a).b=3+((−3a±3(√3))/a) ⇒abc=3a−3a±3(√3)=±3(√3) ⇒(abc)^2 =27
Fromthehypothesiswehave:a+3b=c+3a⇒c=a2−3a+3b(1)⇒3c=3aba2b+3a−3b⇒a+3b=b+3aba2b+3a−3b⇒ab+3−b2b=3aba2b+3a−3b⇔a3b2+3a2b−a2b3+3a2b+9a−3ab2−3ab2−9b+3b3=3ab2Aftersimplifycationweobtaina3b2−(b3−6b)a2−(9b2−9)a+3b3−9b=(a−b)(a2b2+6ab−3b2+9)=0.Sincea≠b,wegeta2b2+6ab−3b2+9=0⇔(a2−3)b2+6ab+9=0.∙ifa2−3=0⇔a=±3thenb=−3±23=∓32⇒c=∓23⇒abc=±33⇒(abc)2=27∙ifa2−3≠0.Then△′=9a2−9a2+27=27,sob=−3a±33a2−3.Hencefrom(1)wegetbc=3+a2−3a.b=3+−3a±33a⇒abc=3a−3a±33=±33⇒(abc)2=27
Commented by mr W last updated on 17/Dec/21
thanks sir!
thankssir!
Commented by 1549442205PVT last updated on 18/Dec/21
Thank you Sir Mr.W ,i mistake and corrected
ThankyouSirMr.W,imistakeandcorrected
Answered by mr W last updated on 17/Dec/21
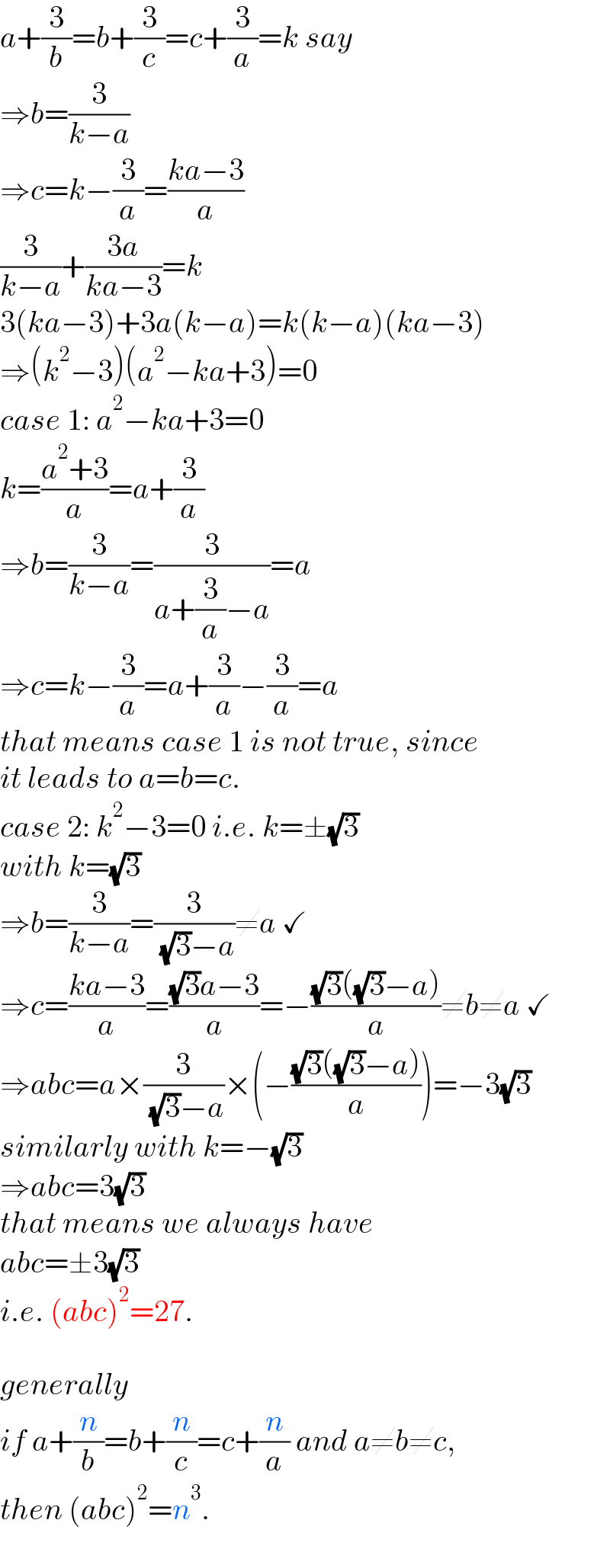
a+(3/b)=b+(3/c)=c+(3/a)=k say ⇒b=(3/(k−a)) ⇒c=k−(3/a)=((ka−3)/a) (3/(k−a))+((3a)/(ka−3))=k 3(ka−3)+3a(k−a)=k(k−a)(ka−3) ⇒(k^2 −3)(a^2 −ka+3)=0 case 1: a^2 −ka+3=0 k=((a^2 +3)/a)=a+(3/a) ⇒b=(3/(k−a))=(3/(a+(3/a)−a))=a ⇒c=k−(3/a)=a+(3/a)−(3/a)=a that means case 1 is not true, since it leads to a=b=c. case 2: k^2 −3=0 i.e. k=±(√3) with k=(√3) ⇒b=(3/(k−a))=(3/( (√3)−a))≠a ✓ ⇒c=((ka−3)/a)=(((√3)a−3)/a)=−(((√3)((√3)−a))/a)≠b≠a ✓ ⇒abc=a×(3/( (√3)−a))×(−(((√3)((√3)−a))/a))=−3(√3) similarly with k=−(√3) ⇒abc=3(√3) that means we always have abc=±3(√3) i.e. (abc)^2 =27. generally if a+(n/b)=b+(n/c)=c+(n/a) and a≠b≠c, then (abc)^2 =n^3 .
a+3b=b+3c=c+3a=ksay⇒b=3k−a⇒c=k−3a=ka−3a3k−a+3aka−3=k3(ka−3)+3a(k−a)=k(k−a)(ka−3)⇒(k2−3)(a2−ka+3)=0case1:a2−ka+3=0k=a2+3a=a+3a⇒b=3k−a=3a+3a−a=a⇒c=k−3a=a+3a−3a=athatmeanscase1isnottrue,sinceitleadstoa=b=c.case2:k2−3=0i.e.k=±3withk=3⇒b=3k−a=33−a≠a✓⇒c=ka−3a=3a−3a=−3(3−a)a≠b≠a✓⇒abc=a×33−a×(−3(3−a)a)=−33similarlywithk=−3⇒abc=33thatmeanswealwayshaveabc=±33i.e.(abc)2=27.generallyifa+nb=b+nc=c+naanda≠b≠c,then(abc)2=n3.
Commented by Tawa11 last updated on 17/Dec/21
Great sir.
Greatsir.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *