Menu Close

simlify-A-1-2-5-4-1-2-5-4-B-1-3-2-6-1-3-2-6-

Tinku Tara 0 Comments
Pin




Question Number 38517 by math khazana by abdo last updated on 26/Jun/18
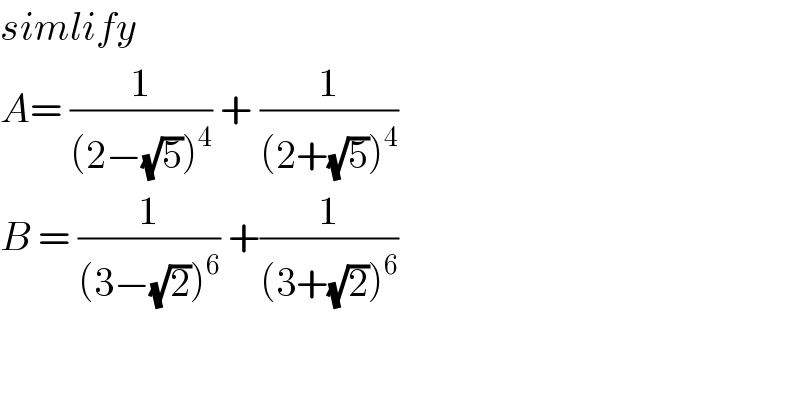
simlify A= (1/((2−(√5))^4 )) + (1/((2+(√5))^4 )) B = (1/((3−(√2))^6 )) +(1/((3+(√2))^6 ))
$${simlify} \\ $$$${A}=\:\frac{\mathrm{1}}{\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)^{\mathrm{4}} }\:+\:\frac{\mathrm{1}}{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{4}} } \\ $$$${B}\:=\:\frac{\mathrm{1}}{\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)^{\mathrm{6}} }\:+\frac{\mathrm{1}}{\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)^{\mathrm{6}} } \\ $$
Answered by MJS last updated on 26/Jun/18
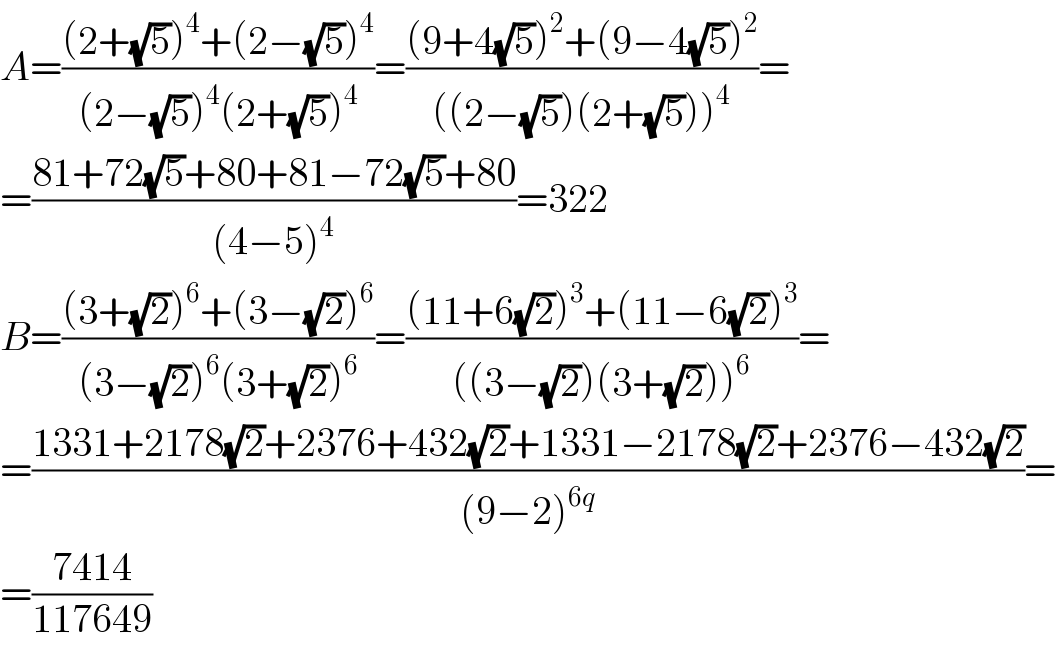
A=(((2+(√5))^4 +(2−(√5))^4 )/((2−(√5))^4 (2+(√5))^4 ))=(((9+4(√5))^2 +(9−4(√5))^2 )/(((2−(√5))(2+(√5)))^4 ))= =((81+72(√5)+80+81−72(√5)+80)/((4−5)^4 ))=322 B=(((3+(√2))^6 +(3−(√2))^6 )/((3−(√2))^6 (3+(√2))^6 ))=(((11+6(√2))^3 +(11−6(√2))^3 )/(((3−(√2))(3+(√2)))^6 ))= =((1331+2178(√2)+2376+432(√2)+1331−2178(√2)+2376−432(√2))/((9−2)^(6q) ))= =((7414)/(117649))
$${A}=\frac{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{4}} +\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)^{\mathrm{4}} }{\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)^{\mathrm{4}} \left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{4}} }=\frac{\left(\mathrm{9}+\mathrm{4}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} +\left(\mathrm{9}−\mathrm{4}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\left(\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\right)^{\mathrm{4}} }= \\ $$$$=\frac{\mathrm{81}+\mathrm{72}\sqrt{\mathrm{5}}+\mathrm{80}+\mathrm{81}−\mathrm{72}\sqrt{\mathrm{5}}+\mathrm{80}}{\left(\mathrm{4}−\mathrm{5}\right)^{\mathrm{4}} }=\mathrm{322} \\ $$$${B}=\frac{\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)^{\mathrm{6}} +\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)^{\mathrm{6}} }{\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)^{\mathrm{6}} \left(\mathrm{3}+\sqrt{\mathrm{2}}\right)^{\mathrm{6}} }=\frac{\left(\mathrm{11}+\mathrm{6}\sqrt{\mathrm{2}}\right)^{\mathrm{3}} +\left(\mathrm{11}−\mathrm{6}\sqrt{\mathrm{2}}\right)^{\mathrm{3}} }{\left(\left(\mathrm{3}−\sqrt{\mathrm{2}}\right)\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)\right)^{\mathrm{6}} }= \\ $$$$=\frac{\mathrm{1331}+\mathrm{2178}\sqrt{\mathrm{2}}+\mathrm{2376}+\mathrm{432}\sqrt{\mathrm{2}}+\mathrm{1331}−\mathrm{2178}\sqrt{\mathrm{2}}+\mathrm{2376}−\mathrm{432}\sqrt{\mathrm{2}}}{\left(\mathrm{9}−\mathrm{2}\right)^{\mathrm{6}{q}} }= \\ $$$$=\frac{\mathrm{7414}}{\mathrm{117649}} \\ $$
Commented by math khazana by abdo last updated on 26/Jun/18
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$
Answered by math1967 last updated on 27/Jun/18
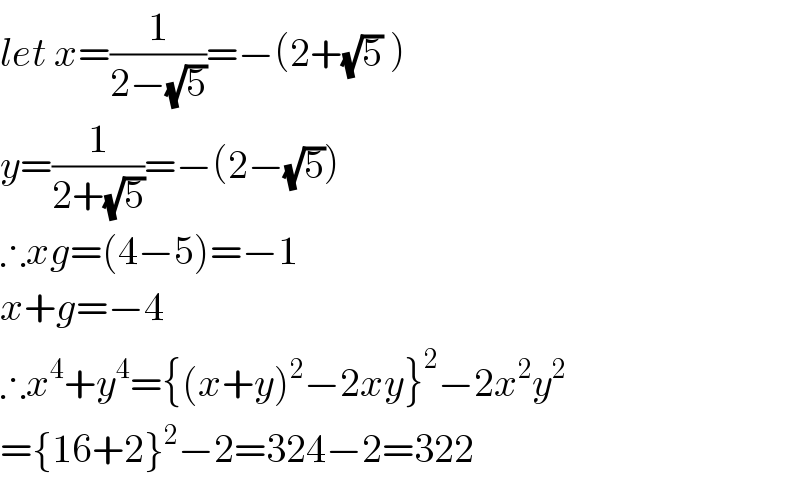
let x=(1/(2−(√5)))=−(2+(√5) ) y=(1/(2+(√5)))=−(2−(√5)) ∴xg=(4−5)=−1 x+g=−4 ∴x^4 +y^4 ={(x+y)^2 −2xy}^2 −2x^2 y^2 ={16+2}^2 −2=324−2=322
$${let}\:{x}=\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{5}}}=−\left(\mathrm{2}+\sqrt{\mathrm{5}}\:\right) \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{5}}}=−\left(\mathrm{2}−\sqrt{\mathrm{5}}\right) \\ $$$$\therefore{xg}=\left(\mathrm{4}−\mathrm{5}\right)=−\mathrm{1} \\ $$$${x}+{g}=−\mathrm{4} \\ $$$$\therefore{x}^{\mathrm{4}} +{y}^{\mathrm{4}} =\left\{\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}\right\}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$=\left\{\mathrm{16}+\mathrm{2}\right\}^{\mathrm{2}} −\mathrm{2}=\mathrm{324}−\mathrm{2}=\mathrm{322} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *