Question Number 147933 by mathdanisur last updated on 24/Jul/21
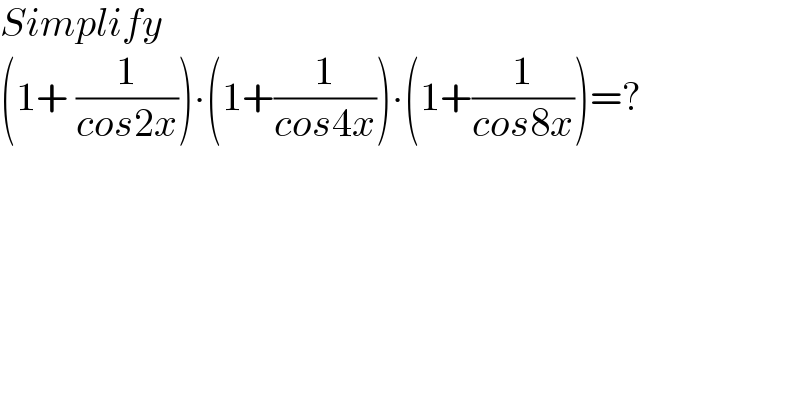
$${Simplify} \\ $$$$\left(\mathrm{1}+\:\frac{\mathrm{1}}{{cos}\mathrm{2}{x}}\right)\centerdot\left(\mathrm{1}+\frac{\mathrm{1}}{{cos}\mathrm{4}{x}}\right)\centerdot\left(\mathrm{1}+\frac{\mathrm{1}}{{cos}\mathrm{8}{x}}\right)=? \\ $$
Answered by som(math1967) last updated on 24/Jul/21
![((tanx)/(tanx))(1+((1+tan^2 x)/(1−tan^2 x)))(1+((1+tan^2 2x)/(1−tan^2 2x))) ×(1+((1+tan^2 4x)/(1−tan^2 4x))) =(1/(tanx))(((2tanx)/(1−tan^2 x)))((2/(1−tan^2 2x)))((2/(1−tan^2 4x))) =(1/(tanx))×((2tan2x)/(1−tan^2 2x))×(2/(1−tan^2 4x)) =(1/(tanx))×((2tan4x)/(1−tan^2 4x))=((tan8x)/(tanx)) [∵tan2x=((2tanx)/(1−tan^2 x))]](https://www.tinkutara.com/question/Q147954.png)
$$\frac{{tanx}}{{tanx}}\left(\mathrm{1}+\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}+{tan}^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{2}{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:×\left(\mathrm{1}+\frac{\mathrm{1}+{tan}^{\mathrm{2}} \mathrm{4}{x}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{4}{x}}\right) \\ $$$$=\frac{\mathrm{1}}{{tanx}}\left(\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\right)\left(\frac{\mathrm{2}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{2}{x}}\right)\left(\frac{\mathrm{2}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{4}{x}}\right) \\ $$$$=\frac{\mathrm{1}}{{tanx}}×\frac{\mathrm{2}{tan}\mathrm{2}{x}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{2}{x}}×\frac{\mathrm{2}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{4}{x}} \\ $$$$=\frac{\mathrm{1}}{{tanx}}×\frac{\mathrm{2}{tan}\mathrm{4}{x}}{\mathrm{1}−{tan}^{\mathrm{2}} \mathrm{4}{x}}=\frac{{tan}\mathrm{8}{x}}{{tanx}} \\ $$$$\left[\because{tan}\mathrm{2}{x}=\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}\right] \\ $$
Commented by mathdanisur last updated on 24/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
