Question Number 45546 by Tawa1 last updated on 14/Oct/18
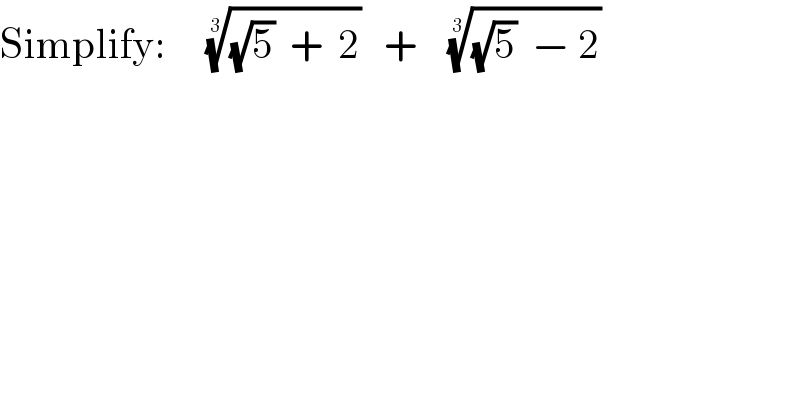
$$\mathrm{Simplify}:\:\:\:\:\:\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{5}}\:\:+\:\:\mathrm{2}}\:\:\:+\:\:\:\:\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{5}}\:\:−\:\mathrm{2}}\:\: \\ $$
Commented by Meritguide1234 last updated on 14/Oct/18
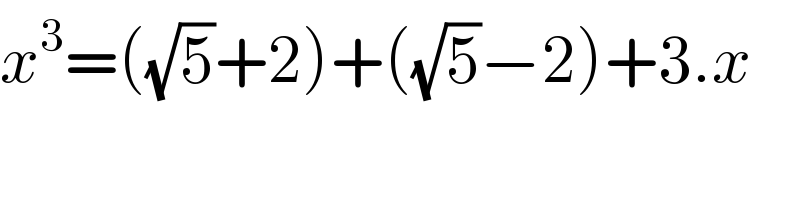
$${x}^{\mathrm{3}} =\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)+\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)+\mathrm{3}.{x} \\ $$$$ \\ $$
Answered by Meritguide1234 last updated on 14/Oct/18
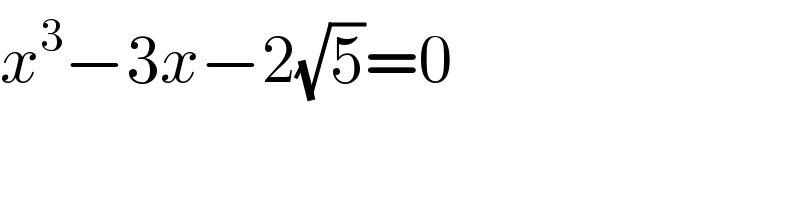
$${x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}\sqrt{\mathrm{5}}=\mathrm{0} \\ $$
Commented by Meritguide1234 last updated on 14/Oct/18
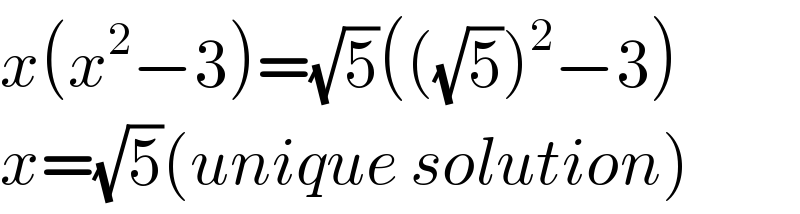
$${x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)=\sqrt{\mathrm{5}}\left(\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{3}\right) \\ $$$${x}=\sqrt{\mathrm{5}}\left({unique}\:{solution}\right) \\ $$
Answered by MJS last updated on 14/Oct/18
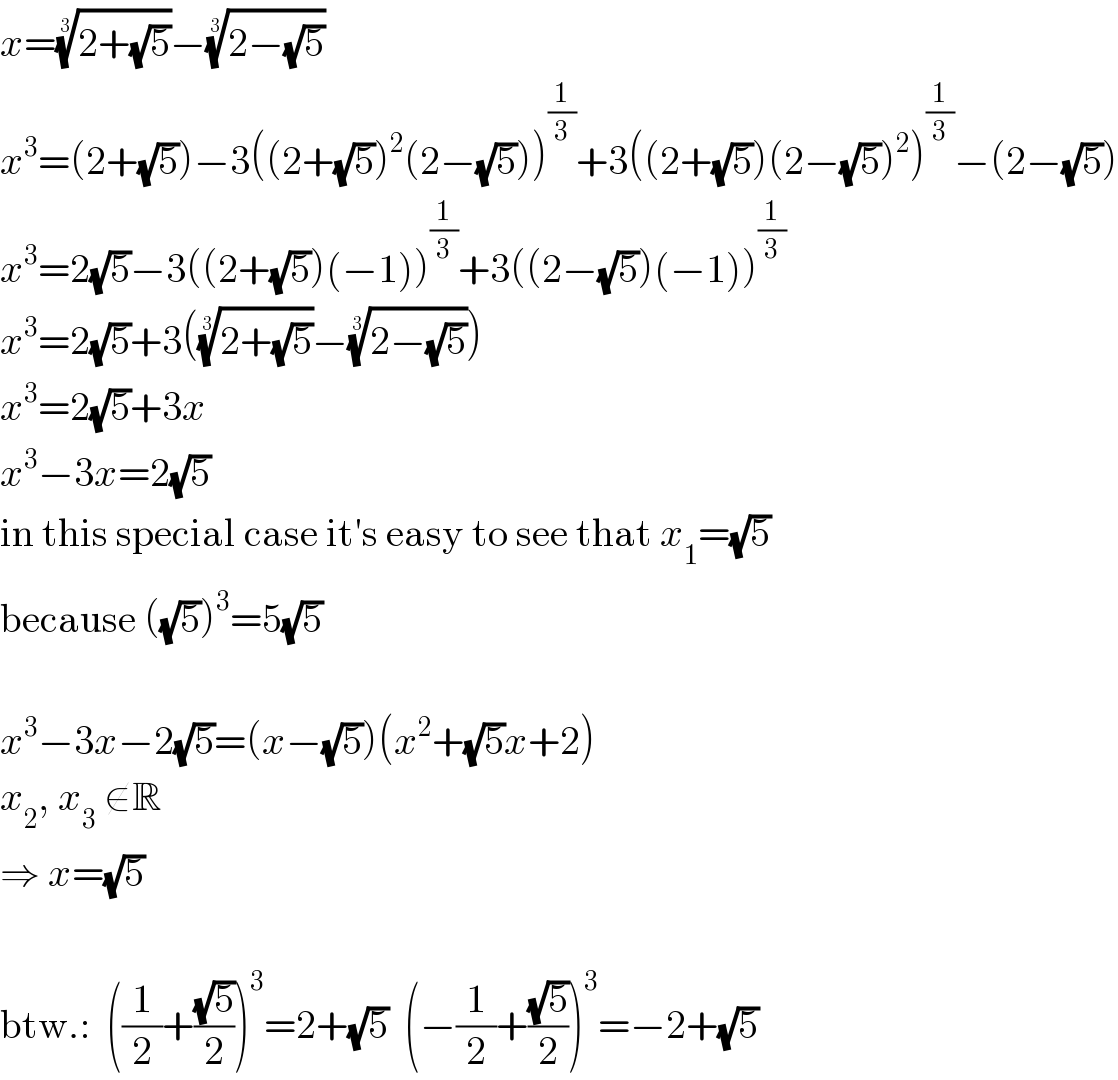
$${x}=\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}−\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}} \\ $$$${x}^{\mathrm{3}} =\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)−\mathrm{3}\left(\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} \left(\mathrm{2}−\sqrt{\mathrm{5}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{3}\left(\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\mathrm{2}−\sqrt{\mathrm{5}}\right) \\ $$$${x}^{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{3}\left(\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\left(−\mathrm{1}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{3}\left(\left(\mathrm{2}−\sqrt{\mathrm{5}}\right)\left(−\mathrm{1}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${x}^{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}−\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\right) \\ $$$${x}^{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{3}{x} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{special}\:\mathrm{case}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:{x}_{\mathrm{1}} =\sqrt{\mathrm{5}} \\ $$$$\mathrm{because}\:\left(\sqrt{\mathrm{5}}\right)^{\mathrm{3}} =\mathrm{5}\sqrt{\mathrm{5}} \\ $$$$ \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}\sqrt{\mathrm{5}}=\left({x}−\sqrt{\mathrm{5}}\right)\left({x}^{\mathrm{2}} +\sqrt{\mathrm{5}}{x}+\mathrm{2}\right) \\ $$$${x}_{\mathrm{2}} ,\:{x}_{\mathrm{3}} \:\notin\mathbb{R} \\ $$$$\Rightarrow\:{x}=\sqrt{\mathrm{5}} \\ $$$$ \\ $$$$\mathrm{btw}.:\:\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{2}+\sqrt{\mathrm{5}}\:\:\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} =−\mathrm{2}+\sqrt{\mathrm{5}} \\ $$
Commented by Tawa1 last updated on 14/Oct/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
