Question Number 149778 by mathdanisur last updated on 07/Aug/21
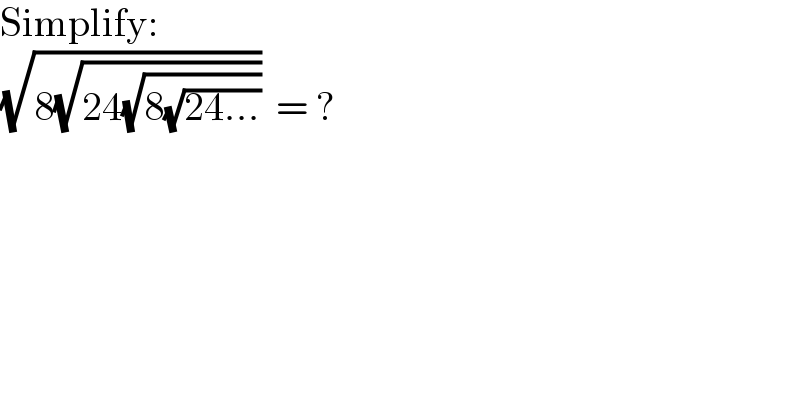
$$\mathrm{Simplify}: \\ $$$$\sqrt{\mathrm{8}\sqrt{\mathrm{24}\sqrt{\mathrm{8}\sqrt{\mathrm{24}…}}}}\:\:=\:? \\ $$
Commented by amin96 last updated on 07/Aug/21
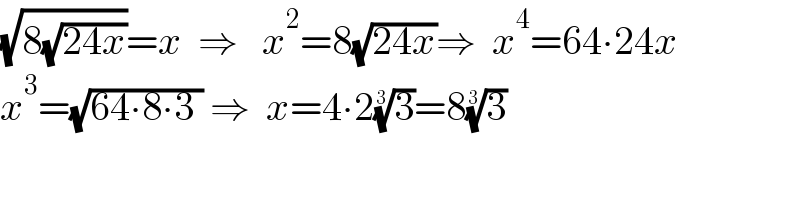
$$\sqrt{\mathrm{8}\sqrt{\mathrm{24}{x}}}={x}\:\:\Rightarrow\:\:\:{x}^{\mathrm{2}} =\mathrm{8}\sqrt{\mathrm{24}{x}}\Rightarrow\:\:{x}^{\mathrm{4}} =\mathrm{64}\centerdot\mathrm{24}{x} \\ $$$${x}^{\mathrm{3}} =\sqrt{\mathrm{64}\centerdot\mathrm{8}\centerdot\mathrm{3}\:}\:\Rightarrow\:\:{x}=\mathrm{4}\centerdot\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{3}}=\mathrm{8}\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 07/Aug/21

$${Thanks}\:{Ser} \\ $$
Answered by nimnim last updated on 07/Aug/21
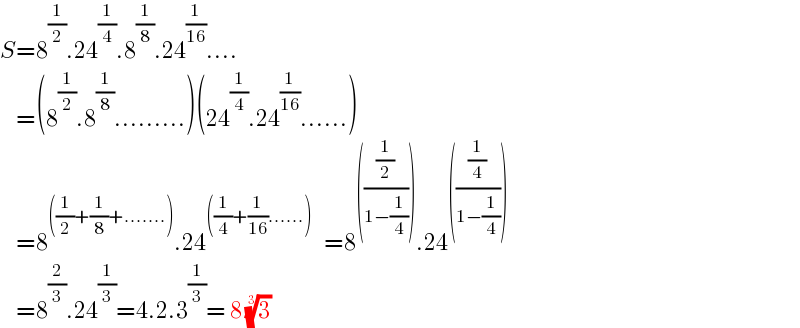
$${S}=\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{24}^{\frac{\mathrm{1}}{\mathrm{4}}} .\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{8}}} .\mathrm{24}^{\frac{\mathrm{1}}{\mathrm{16}}} …. \\ $$$$\:\:\:\:=\left(\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{8}^{\frac{\mathrm{1}}{\mathrm{8}}} ………\right)\left(\mathrm{24}^{\frac{\mathrm{1}}{\mathrm{4}}} .\mathrm{24}^{\frac{\mathrm{1}}{\mathrm{16}}} ……\right) \\ $$$$\:\:\:\:=\mathrm{8}^{\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{8}}+…….\right)} .\mathrm{24}^{\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}}……\right)} \:\:\:=\mathrm{8}^{\left(\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}\right)} .\mathrm{24}^{\left(\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}\right)} \\ $$$$\:\:\:\:=\mathrm{8}^{\frac{\mathrm{2}}{\mathrm{3}}} .\mathrm{24}^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{4}.\mathrm{2}.\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{3}}} =\:\mathrm{8}\:\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$
Commented by lyubita last updated on 07/Aug/21

$${great}… \\ $$
Commented by mathdanisur last updated on 07/Aug/21

$${Thanks}\:{Ser} \\ $$
