Question Number 172513 by Mikenice last updated on 28/Jun/22

$${simplify} \\ $$$$\sqrt{{a}^{\mathrm{2}} {b}+{b}^{\mathrm{3}} +\mathrm{2}{ab}^{\mathrm{2}} }\:−\sqrt{{a}^{\mathrm{2}} {b}+\mathrm{4}{b}^{\mathrm{3}} +\mathrm{4}{ab}^{\mathrm{3}} } \\ $$
Commented by Rasheed.Sindhi last updated on 28/Jun/22

$$\mathcal{D}{o}\:{you}\:{mean}: \\ $$$$\sqrt{{a}^{\mathrm{2}} {b}+{b}^{\mathrm{3}} +\mathrm{2}{ab}^{\mathrm{2}} }\:−\sqrt{{a}^{\mathrm{2}} {b}+\mathrm{4}{b}^{\mathrm{3}} +\mathrm{4}{ab}^{\mathrm{2}} } \\ $$
Commented by Mikenice last updated on 28/Jun/22

$${yes} \\ $$
Answered by Rasheed.Sindhi last updated on 28/Jun/22
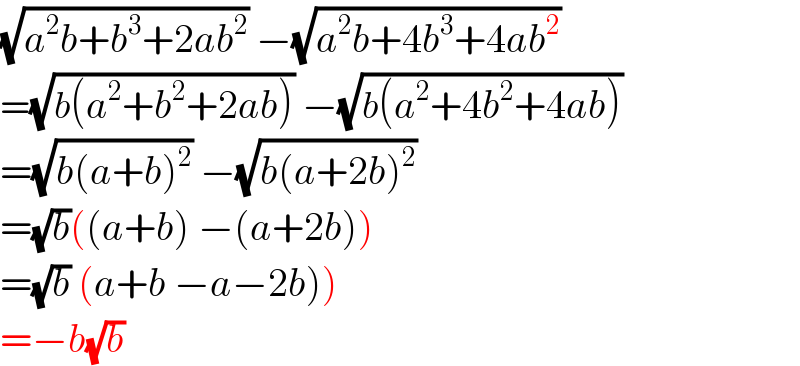
$$\sqrt{{a}^{\mathrm{2}} {b}+{b}^{\mathrm{3}} +\mathrm{2}{ab}^{\mathrm{2}} }\:−\sqrt{{a}^{\mathrm{2}} {b}+\mathrm{4}{b}^{\mathrm{3}} +\mathrm{4}{ab}^{\mathrm{2}} } \\ $$$$=\sqrt{{b}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\right)}\:−\sqrt{{b}\left({a}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} +\mathrm{4}{ab}\right)} \\ $$$$=\sqrt{{b}\left({a}+{b}\right)^{\mathrm{2}} }\:−\sqrt{{b}\left({a}+\mathrm{2}{b}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{{b}}\left(\left({a}+{b}\right)\:−\left({a}+\mathrm{2}{b}\right)\right) \\ $$$$\left.=\sqrt{{b}}\:\left({a}+{b}\:−{a}−\mathrm{2}{b}\right)\right) \\ $$$$=−{b}\sqrt{{b}} \\ $$
Answered by MJS_new last updated on 28/Jun/22

$$\sqrt{{a}^{\mathrm{2}} {b}+{b}^{\mathrm{3}} +\mathrm{2}{ab}^{\mathrm{2}} }=\mid{a}+{b}\mid\sqrt{{b}} \\ $$$$\sqrt{{a}^{\mathrm{2}} {b}+\mathrm{4}{b}^{\mathrm{3}} +\mathrm{4}{ab}^{\mathrm{2}} }=\mid{a}+\mathrm{2}{b}\mid\sqrt{{b}} \\ $$$$\mathrm{different}\:\mathrm{results}\:\mathrm{depending}\:\mathrm{on}\:{a}+{b}\:\mathrm{and} \\ $$$${a}+\mathrm{2}{b}\:>=<\mathrm{0} \\ $$
