Menu Close

simplify-A-n-k-0-n-k-2-C-n-k-cos-k-and-B-n-k-0-n-k-2-C-n-k-sin-k-

Tinku Tara 0 Comments
Pin




Question Number 54675 by maxmathsup by imad last updated on 09/Feb/19
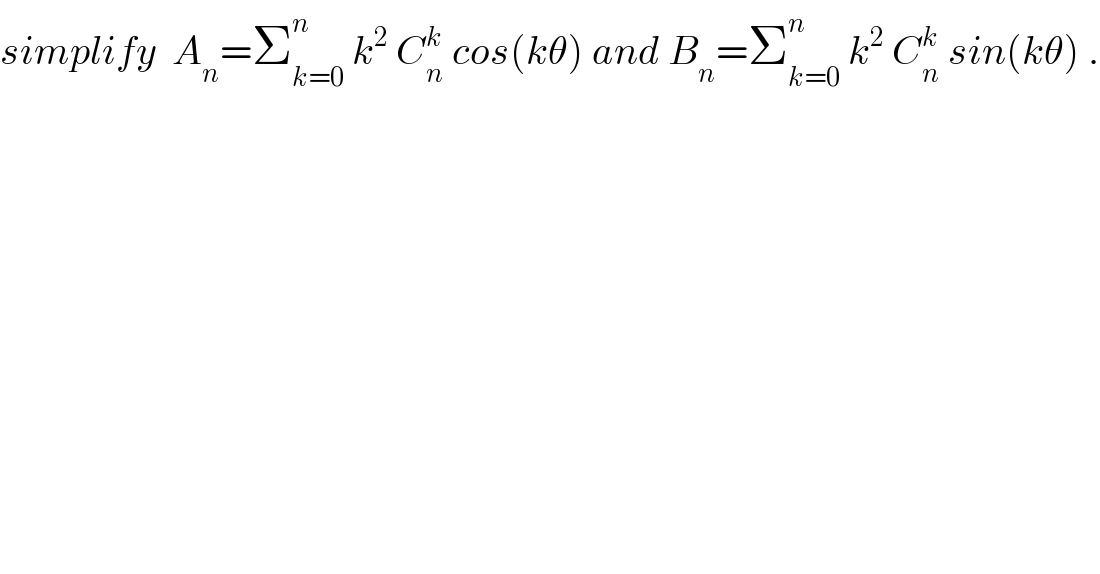
simplify A_n =Σ_(k=0) ^n k^2 C_n ^k cos(kθ) and B_n =Σ_(k=0) ^n k^2 C_n ^k sin(kθ) .
$${simplify}\:\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:{cos}\left({k}\theta\right)\:{and}\:{B}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:{sin}\left({k}\theta\right)\:. \\ $$
Commented by maxmathsup by imad last updated on 10/Feb/19
we have A_n +iB_n =Σ_(k=0) ^n k^2 C_n ^k (e^(iθ) )^k but we have proved that Σ_(k=0) ^n k^2 C_n ^k z^k = nz(z+1)^(n−1) +n(n−1)z^2 (z+1)^(n−2) ⇒ Σ_(k=0) ^n k^2 C_n ^k (e^(iθ) )^k =n e^(iθ) (1+e^(iθ) )^(n−1) +n(n−1)e^(2iθ) (e^(iθ) +1)^(n−2) but 1+e^(iθ) =1+cosθ +isinθ =2cos^2 ((θ/2)) +2isin((θ/2))cos((θ/2)) =2cos((θ/2))e^(i(θ/2)) ⇒ A_n +iB_n =n e^(iθ) 2^(n−1) cos^(n−1) ((θ/2))e^(i((nθ)/2)) +n(n−1)e^(2iθ) 2^(n−2) cos^(n−2) ((θ/2))e^(i(((n−2)θ)/2)) =n 2^(n−1) cos^(n−1)) ((θ/2)) e^(i(θ +((nθ)/2))) +n(n−1) 2^(n−2) e^(i(2θ +(((n−2)θ)/2))) =n 2^(n−1) cos^(n−1) ((θ/2)){cos((((n+2)θ)/2))+isin((((n+2)θ)/2))} +n(n−1)2^(n−2) {cos((((n+2)θ)/2)) +isin((((n+2)θ)/2)) =(n 2^(n−1) cos^(n−1) ((θ/2)) +n(n−1)2^(n−2) )cos((((n+2)θ)/2)) +i (n 2^(n−1) cos^(n−1) ((θ/2)) +n(n−1)2^(n−2) )sin((((n+2)θ)/2)) ⇒ A_n =(n 2^(n−1) cos^(n−1) ((θ/2))+n(n−1)2^(n−2) )cos((((n+2)θ)/2)) and B_n =(n 2^(n−1) cos^(n−1) ((θ/2))+n(n−1)2^(n−2) )sin((((n+2)θ)/2)) .
$${we}\:{have}\:{A}_{{n}} +{iB}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:\:\left({e}^{{i}\theta} \right)^{{k}} \:\:\:{but}\:{we}\:{have}\:{proved}\:{that} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:{z}^{{k}} \:\:\:=\:{nz}\left({z}+\mathrm{1}\right)^{{n}−\mathrm{1}} \:\:+{n}\left({n}−\mathrm{1}\right){z}^{\mathrm{2}} \left({z}+\mathrm{1}\right)^{{n}−\mathrm{2}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:\left({e}^{{i}\theta} \right)^{{k}} \:={n}\:{e}^{{i}\theta} \left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{1}} \:+{n}\left({n}−\mathrm{1}\right){e}^{\mathrm{2}{i}\theta} \left({e}^{{i}\theta} \:+\mathrm{1}\right)^{{n}−\mathrm{2}} \:\:{but} \\ $$$$\mathrm{1}+{e}^{{i}\theta} \:=\mathrm{1}+{cos}\theta\:+{isin}\theta\:=\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\:+\mathrm{2}{isin}\left(\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}{cos}\left(\frac{\theta}{\mathrm{2}}\right){e}^{{i}\frac{\theta}{\mathrm{2}}} \:\Rightarrow\:{A}_{{n}} +{iB}_{{n}} ={n}\:{e}^{{i}\theta} \mathrm{2}^{{n}−\mathrm{1}} {cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right){e}^{{i}\frac{{n}\theta}{\mathrm{2}}} \\ $$$$+{n}\left({n}−\mathrm{1}\right){e}^{\mathrm{2}{i}\theta} \:\:\mathrm{2}^{{n}−\mathrm{2}} \:{cos}^{{n}−\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right){e}^{{i}\frac{\left({n}−\mathrm{2}\right)\theta}{\mathrm{2}}} \\ $$$$={n}\:\mathrm{2}^{{n}−\mathrm{1}} \:{cos}^{\left.{n}−\mathrm{1}\right)} \left(\frac{\theta}{\mathrm{2}}\right)\:{e}^{{i}\left(\theta\:+\frac{{n}\theta}{\mathrm{2}}\right)} \:\:+{n}\left({n}−\mathrm{1}\right)\:\mathrm{2}^{{n}−\mathrm{2}} \:{e}^{{i}\left(\mathrm{2}\theta\:+\frac{\left({n}−\mathrm{2}\right)\theta}{\mathrm{2}}\right)} \\ $$$$={n}\:\mathrm{2}^{{n}−\mathrm{1}} \:{cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)\left\{{cos}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)+{isin}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)\right\} \\ $$$$+{n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \:\:\left\{{cos}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)\:+{isin}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)\right. \\ $$$$=\left({n}\:\mathrm{2}^{{n}−\mathrm{1}} \:{cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)\:+{n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \right){cos}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right) \\ $$$$+{i}\:\left({n}\:\mathrm{2}^{{n}−\mathrm{1}} \:{cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)\:+{n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \right){sin}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\left({n}\:\mathrm{2}^{{n}−\mathrm{1}} {cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)+{n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \right){cos}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)\:{and} \\ $$$${B}_{{n}} =\left({n}\:\mathrm{2}^{{n}−\mathrm{1}} \:{cos}^{{n}−\mathrm{1}} \left(\frac{\theta}{\mathrm{2}}\right)+{n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \right){sin}\left(\frac{\left({n}+\mathrm{2}\right)\theta}{\mathrm{2}}\right)\:. \\ $$
Answered by Smail last updated on 09/Feb/19
A_n +iB_n =S′′(θ) S′′(θ)=Σ_(k=0) ^n k^2 C_n ^k e^(iθk) S′(θ)=(1/i)Σ_(k=0) ^n kC_n ^k e^(iθk) +c_1 S(θ)=−Σ_(k=0) ^n C_n ^k e^(iθk) +θc_1 +c_2 S(θ)=−(1+e^(iθ) )^n +θc_1 +c_2 S′(θ)=−ine^(iθ) (1+e^(iθ) )^(n−1) +c_1 S′′(θ)=ne^(iθ) (1+e^(iθ) )^(n−1) +n(n−1)e^(2iθ) (1+e^(iθ) )^(n−2) =ne^(iθ) (1+e^(iθ) )^(n−2) (1+e^(iθ) +(n−1)e^(iθ) ) A_n +iB_n =ne^(iθ) (1+e^(iθ) )^(n−2) (1+ne^(iθ) ) =ne^(iθ) (1+cosθ+isinθ)^(n−2) (1+ne^(iθ) ) =ne^(iθ) (2cos^2 (θ/2)+2isin((θ/2))cos((θ/2)))^(n−2) (1+ne^(iθ) ) =2^(n−2) ne^(iθ) cos^(n−2) (θ/2)(cos(θ/2)+isin(θ/2))^(n−2) (1+ne^(iθ) ) =2^(n−2) ne^(iθ) cos^(n−2) (θ/2)(e^(i((n−2)/2)θ) )(1+ne^(iθ) ) =2^(n−2) ncos^(n−2) ((θ/2))e^(i(n/2)θ) (1+ne^(iθ) ) =2^(n−2) ncos^(n−2) ((θ/2))(e^(i(n/2)θ) +ne^(i((n+2)/2)θ) ) =2^(n−2) ncos^(n−2) ((θ/2))(cos((nθ)/2)+isin((nθ)/2)+ncos((n+2)/2)θ+insin((n+2)/2)θ) A_n =2^(n−2) ncos^(n−2) (θ/2)(cos((nθ)/2)+ncos((n+2)/2)θ) B_n =2^(n−2) ncos^(n−2) (θ/2)(sin((nθ)/2)+nsin((n+2)/2)θ)
$${A}_{{n}} +{iB}_{{n}} ={S}''\left(\theta\right) \\ $$$${S}''\left(\theta\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} {C}_{{n}} ^{{k}} {e}^{{i}\theta{k}} \\ $$$${S}'\left(\theta\right)=\frac{\mathrm{1}}{{i}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kC}_{{n}} ^{{k}} {e}^{{i}\theta{k}} +{c}_{\mathrm{1}} \\ $$$${S}\left(\theta\right)=−\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{n}} ^{{k}} {e}^{{i}\theta{k}} +\theta{c}_{\mathrm{1}} +{c}_{\mathrm{2}} \\ $$$${S}\left(\theta\right)=−\left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}} +\theta{c}_{\mathrm{1}} +{c}_{\mathrm{2}} \\ $$$${S}'\left(\theta\right)=−{ine}^{{i}\theta} \left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{1}} +{c}_{\mathrm{1}} \\ $$$${S}''\left(\theta\right)={ne}^{{i}\theta} \left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{1}} +{n}\left({n}−\mathrm{1}\right){e}^{\mathrm{2}{i}\theta} \left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{2}} \\ $$$$={ne}^{{i}\theta} \left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{2}} \left(\mathrm{1}+{e}^{{i}\theta} +\left({n}−\mathrm{1}\right){e}^{{i}\theta} \right) \\ $$$${A}_{{n}} +{iB}_{{n}} ={ne}^{{i}\theta} \left(\mathrm{1}+{e}^{{i}\theta} \right)^{{n}−\mathrm{2}} \left(\mathrm{1}+{ne}^{{i}\theta} \right) \\ $$$$={ne}^{{i}\theta} \left(\mathrm{1}+{cos}\theta+{isin}\theta\right)^{{n}−\mathrm{2}} \left(\mathrm{1}+{ne}^{{i}\theta} \right) \\ $$$$={ne}^{{i}\theta} \left(\mathrm{2}{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{2}{isin}\left(\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}}\right)\right)^{{n}−\mathrm{2}} \left(\mathrm{1}+{ne}^{{i}\theta} \right) \\ $$$$=\mathrm{2}^{{n}−\mathrm{2}} {ne}^{{i}\theta} {cos}^{{n}−\mathrm{2}} \frac{\theta}{\mathrm{2}}\left({cos}\frac{\theta}{\mathrm{2}}+{isin}\frac{\theta}{\mathrm{2}}\right)^{{n}−\mathrm{2}} \left(\mathrm{1}+{ne}^{{i}\theta} \right) \\ $$$$=\mathrm{2}^{{n}−\mathrm{2}} {ne}^{{i}\theta} {cos}^{{n}−\mathrm{2}} \frac{\theta}{\mathrm{2}}\left({e}^{{i}\frac{{n}−\mathrm{2}}{\mathrm{2}}\theta} \right)\left(\mathrm{1}+{ne}^{{i}\theta} \right) \\ $$$$=\mathrm{2}^{{n}−\mathrm{2}} {ncos}^{{n}−\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right){e}^{{i}\frac{{n}}{\mathrm{2}}\theta} \left(\mathrm{1}+{ne}^{{i}\theta} \right) \\ $$$$=\mathrm{2}^{{n}−\mathrm{2}} {ncos}^{{n}−\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\left({e}^{{i}\frac{{n}}{\mathrm{2}}\theta} +{ne}^{{i}\frac{{n}+\mathrm{2}}{\mathrm{2}}\theta} \right) \\ $$$$=\mathrm{2}^{{n}−\mathrm{2}} {ncos}^{{n}−\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\left({cos}\frac{{n}\theta}{\mathrm{2}}+{isin}\frac{{n}\theta}{\mathrm{2}}+{ncos}\frac{{n}+\mathrm{2}}{\mathrm{2}}\theta+{insin}\frac{{n}+\mathrm{2}}{\mathrm{2}}\theta\right) \\ $$$${A}_{{n}} =\mathrm{2}^{{n}−\mathrm{2}} {ncos}^{{n}−\mathrm{2}} \frac{\theta}{\mathrm{2}}\left({cos}\frac{{n}\theta}{\mathrm{2}}+{ncos}\frac{{n}+\mathrm{2}}{\mathrm{2}}\theta\right) \\ $$$${B}_{{n}} =\mathrm{2}^{{n}−\mathrm{2}} {ncos}^{{n}−\mathrm{2}} \frac{\theta}{\mathrm{2}}\left({sin}\frac{{n}\theta}{\mathrm{2}}+{nsin}\frac{{n}+\mathrm{2}}{\mathrm{2}}\theta\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *