simplify-sin-1-cot-cos-1-tan-

Question Number 105285 by bemath last updated on 27/Jul/20

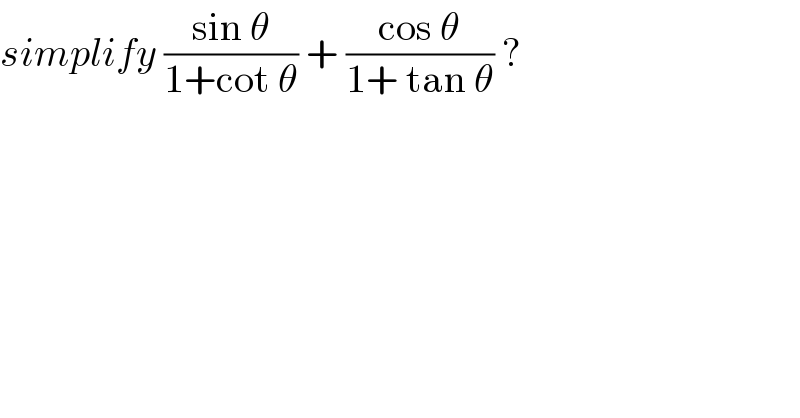
$${simplify}\:\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cot}\:\theta}\:+\:\frac{\mathrm{cos}\:\theta}{\mathrm{1}+\:\mathrm{tan}\:\theta}\:? \\ $$

Commented by bemath last updated on 27/Jul/20

$${thank}\:{you} \\ $$

Commented by som(math1967) last updated on 27/Jul/20

$$\frac{\mathrm{sin}\theta}{\mathrm{1}+\frac{\mathrm{cos}\theta}{\mathrm{sin}\theta}}\:+\frac{\mathrm{cos}\theta}{\mathrm{1}+\frac{\mathrm{sin}\theta}{\mathrm{cos}\theta}} \\ $$$$=\frac{\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{sin}\theta+\mathrm{cos}\theta}\:+\frac{\mathrm{cos}^{\mathrm{2}} \theta}{\mathrm{cos}\theta+\mathrm{sin}\theta} \\ $$$$=\frac{\mathrm{1}}{\mathrm{sin}\theta+\mathrm{cos}\theta}\:\:\left[\because\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{1}\right] \\ $$

Answered by bobhans last updated on 27/Jul/20

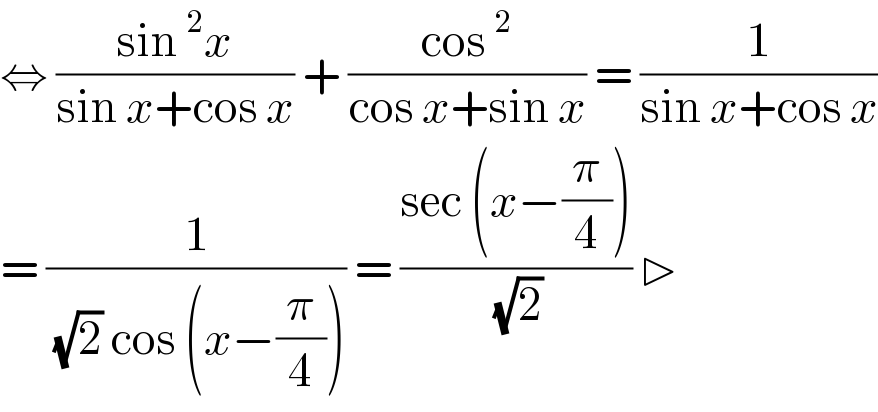
$$\Leftrightarrow\:\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:+\:\frac{\mathrm{cos}\:^{\mathrm{2}} }{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}\:=\:\frac{\mathrm{sec}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}}\:\triangleright \\ $$

Commented by malwaan last updated on 27/Jul/20

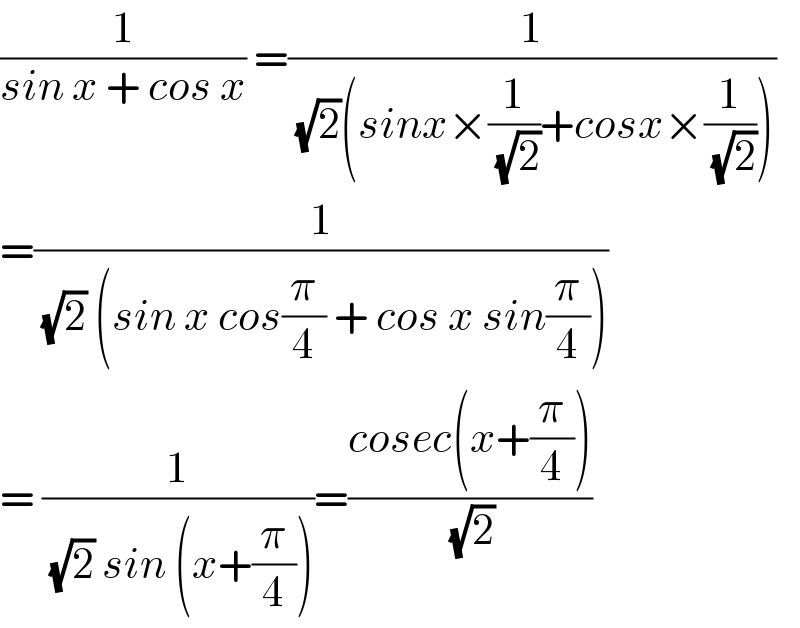
$$\frac{\mathrm{1}}{{sin}\:{x}\:+\:{cos}\:{x}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left({sinx}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+{cosx}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\left({sin}\:{x}\:{cos}\frac{\pi}{\mathrm{4}}\:+\:{cos}\:{x}\:{sin}\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}=\frac{{cosec}\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com