Question Number 155428 by ajfour last updated on 30/Sep/21
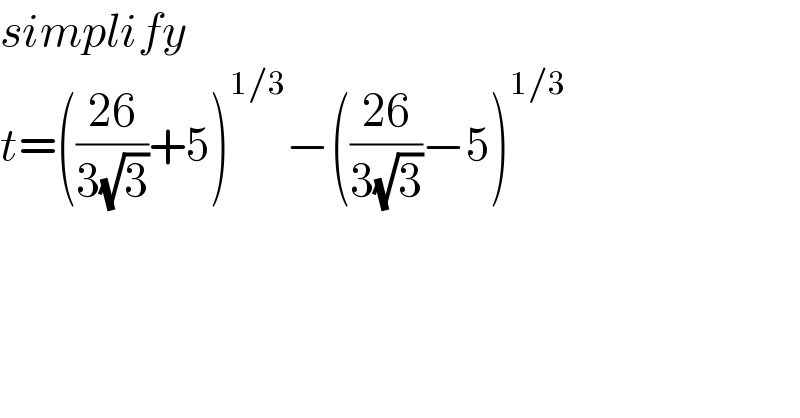
$${simplify} \\ $$$${t}=\left(\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}+\mathrm{5}\right)^{\mathrm{1}/\mathrm{3}} −\left(\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{5}\right)^{\mathrm{1}/\mathrm{3}} \\ $$
Answered by peter frank last updated on 30/Sep/21
![t=(((26+15(√3))/(3(√3))))^(1/3) −(((26−15(√3))/(3(√3))))^(1/3) t=(((26+15(√3))^(1/3) )/(^3 (√(81)) ))−(((26−15(√3) )^(1/3) )/(^3 (√(81)))) t=(1/( (√(81)) ))[(26+15(√3))^(1/3) ]−[(26−15(√3))^(1/3) ] ....](https://www.tinkutara.com/question/Q155437.png)
$$\mathrm{t}=\left(\frac{\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} −\left(\frac{\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\mathrm{t}=\frac{\left(\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\:^{\mathrm{3}} \sqrt{\mathrm{81}}\:}−\frac{\left(\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}\:\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\:^{\mathrm{3}} \sqrt{\mathrm{81}}} \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{81}}\:}\left[\left(\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right]−\left[\left(\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right] \\ $$$$…. \\ $$$$ \\ $$
Answered by som(math1967) last updated on 30/Sep/21
![let a=(((26)/(3(√3)))+5)^(1/3) b=(((26)/(3(√3)))−5)^(1/3) ∴a^3 −b^3 =((26)/(3(√3)))+5−((26)/(3(√3)))+5 a^3 −b^3 =10 ab={((26^2 )/(27))−25}^(1/3) =((1/(27)))^(1/3) =(1/3) (a−b)^3 =a^3 −b^3 −3ab(a−b) x^3 =10−3×(1/3)×x [let (a−b)=x] x^3 +x−10=0 x^3 −2x^2 +2x^2 −4x+5x−10=0 (x−2)(x^2 +2x+5)=0 x=2 [taking real value only] ∴a−b=2 ∴(((26)/(3(√3))) +5)^(1/3) +(((26)/(3(√3))) −5)^(1/3) =2](https://www.tinkutara.com/question/Q155442.png)
$${let}\:{a}=\left(\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}+\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:{b}=\left(\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\therefore{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}+\mathrm{5}−\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}+\mathrm{5} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{10} \\ $$$${ab}=\left\{\frac{\mathrm{26}^{\mathrm{2}} }{\mathrm{27}}−\mathrm{25}\right\}^{\frac{\mathrm{1}}{\mathrm{3}}} =\left(\frac{\mathrm{1}}{\mathrm{27}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} −{b}^{\mathrm{3}} −\mathrm{3}{ab}\left({a}−{b}\right) \\ $$$${x}^{\mathrm{3}} =\mathrm{10}−\mathrm{3}×\frac{\mathrm{1}}{\mathrm{3}}×{x}\:\left[{let}\:\left({a}−{b}\right)={x}\right] \\ $$$${x}^{\mathrm{3}} +{x}−\mathrm{10}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}{x}−\mathrm{10}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)=\mathrm{0} \\ $$$${x}=\mathrm{2}\:\left[{taking}\:{real}\:{value}\:{only}\right] \\ $$$$\therefore{a}−{b}=\mathrm{2} \\ $$$$\therefore\left(\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}\:+\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\frac{\mathrm{26}}{\mathrm{3}\sqrt{\mathrm{3}}}\:−\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{2} \\ $$
Commented by ajfour last updated on 30/Sep/21

$${thanks}\:{sir},\:{all}\:{too}\:{nice}. \\ $$
