Question Number 93689 by oustmuchiya@gmail.com last updated on 14/May/20
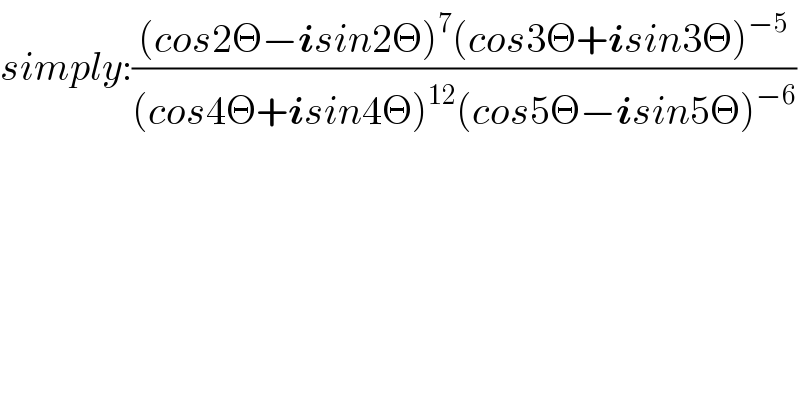
$${simply}:\frac{\left({cos}\mathrm{2}\Theta−\boldsymbol{{i}}{sin}\mathrm{2}\Theta\right)^{\mathrm{7}} \left({cos}\mathrm{3}\Theta+\boldsymbol{{i}}{sin}\mathrm{3}\Theta\right)^{−\mathrm{5}} }{\left({cos}\mathrm{4}\Theta+\boldsymbol{{i}}{sin}\mathrm{4}\Theta\right)^{\mathrm{12}} \left({cos}\mathrm{5}\Theta−\boldsymbol{{i}}{sin}\mathrm{5}\Theta\right)^{−\mathrm{6}} } \\ $$
Commented by PRITHWISH SEN 2 last updated on 14/May/20
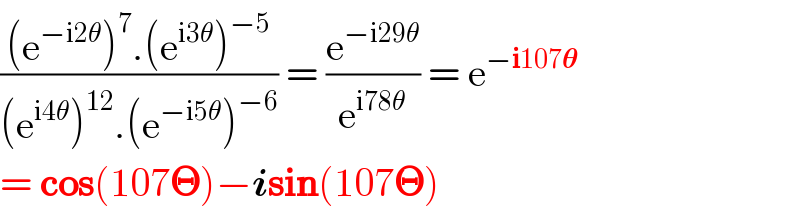
$$\frac{\left(\mathrm{e}^{−\mathrm{i2}\theta} \right)^{\mathrm{7}} .\left(\mathrm{e}^{\mathrm{i3}\theta} \right)^{−\mathrm{5}} }{\left(\mathrm{e}^{\mathrm{i4}\theta} \right)^{\mathrm{12}} .\left(\mathrm{e}^{−\mathrm{i5}\theta} \right)^{−\mathrm{6}} }\:=\:\frac{\mathrm{e}^{−\mathrm{i29}\theta} }{\mathrm{e}^{\mathrm{i78}\theta} }\:=\:\mathrm{e}^{−\boldsymbol{\mathrm{i}}\mathrm{107}\boldsymbol{\theta}} \\ $$$$=\:\boldsymbol{\mathrm{cos}}\left(\mathrm{107}\boldsymbol{\Theta}\right)−\boldsymbol{{i}\mathrm{sin}}\left(\mathrm{107}\boldsymbol{\Theta}\right) \\ $$
