Menu Close

sin-1-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 60783 by aliesam last updated on 25/May/19
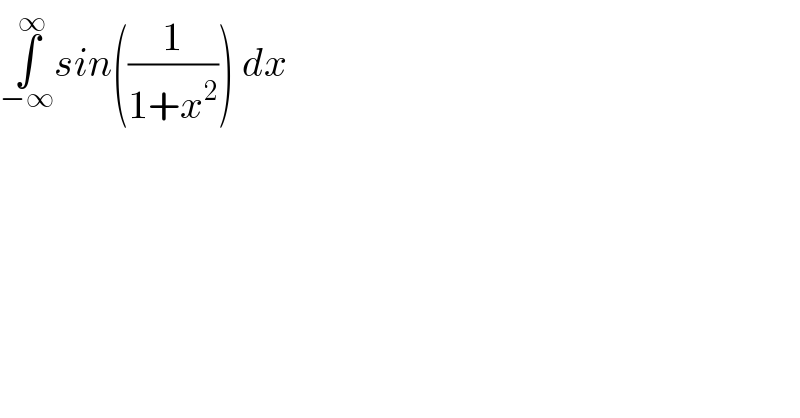
∫_(−∞) ^∞ sin((1/(1+x^2 ))) dx
$$\underset{−\infty} {\overset{\infty} {\int}}{sin}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{dx} \\ $$
Commented by maxmathsup by imad last updated on 25/May/19
let A =∫_(−∞) ^(+∞) sin((1/(1+x^2 )))dx ⇒A =2∫_0 ^∞ sin((1/(1+x^2 )))dx =_(x=tanθ) ∫_0 ^(π/2) sin(cos^2 θ)(1+tan^2 θ)dθ =∫_0 ^(π/2) ((sin(cos^2 θ))/(cos^2 θ)) dθ we have x−(x^3 /6) ≤sinx ≤x for 0<x<(π/2) ⇒ cos^2 θ −(1/6) cos^6 x ≤ sin(cos^2 x) ≤ cos^2 x ⇒ 1−(1/6) cos^4 x ≤((sin(cos^2 x))/(cos^2 x)) ≤1 ⇒ ∫_0 ^(π/2) (1−(1/6) cos^4 x)dx ≤ ∫_0 ^(π/2) ((sin(cos^2 x))/(cos^2 x)) dx ≤(π/2) ⇒ (π/2) −(1/6) ∫_0 ^(π/2) cos^4 x dx ≤A ≤(π/2) ∫_0 ^(π/2) cos^4 x dx =∫_0 ^(π/2) (((1+cos(2x))/2))^2 dx =(1/4) ∫_0 ^(π/2) (1+2cos(2x) +cos^2 (2x))dx =(π/8) +(1/2) ∫_0 ^(π/2) cos(2x)dx +(1/8) ∫_0 ^(π/2) (1+cos(4x))dx =(π/8) +0 +(π/(16)) +9 =((3π)/(16)) ⇒ (π/2) −(π/(32)) ≤ A ≤ (π/2) we can take α_0 =((π−(π/(32)))/2) =((31π)/(64)) as approximatevalue for this integra α_0 ∼1 ,52 .
$${let}\:{A}\:=\int_{−\infty} ^{+\infty} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}\:\:\Rightarrow{A}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {sin}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}\:=_{{x}={tan}\theta} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left({cos}^{\mathrm{2}} \theta\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{sin}\left({cos}^{\mathrm{2}} \theta\right)}{{cos}^{\mathrm{2}} \theta}\:{d}\theta\:\:\:\:\:\:\:{we}\:{have}\:\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:\leqslant{sinx}\:\leqslant{x}\:\:\:{for}\:\mathrm{0}<{x}<\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${cos}^{\mathrm{2}} \theta\:−\frac{\mathrm{1}}{\mathrm{6}}\:{cos}^{\mathrm{6}} {x}\:\leqslant\:{sin}\left({cos}^{\mathrm{2}} {x}\right)\:\leqslant\:{cos}^{\mathrm{2}} {x}\:\Rightarrow\:\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\:{cos}^{\mathrm{4}} {x}\:\leqslant\frac{{sin}\left({cos}^{\mathrm{2}} {x}\right)}{{cos}^{\mathrm{2}} {x}}\:\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\:{cos}^{\mathrm{4}} {x}\right){dx}\:\leqslant\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sin}\left({cos}^{\mathrm{2}} {x}\right)}{{cos}^{\mathrm{2}} {x}}\:{dx}\:\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{6}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{4}} {x}\:{dx}\:\leqslant{A}\:\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{4}} {x}\:{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} {dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{x}\right)\:+{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{x}\right){dx}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{8}}\:+\mathrm{0}\:+\frac{\pi}{\mathrm{16}}\:+\mathrm{9}\:=\frac{\mathrm{3}\pi}{\mathrm{16}}\:\Rightarrow\:\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{32}}\:\leqslant\:{A}\:\leqslant\:\frac{\pi}{\mathrm{2}} \\ $$$${we}\:{can}\:{take}\:\:\alpha_{\mathrm{0}} =\frac{\pi−\frac{\pi}{\mathrm{32}}}{\mathrm{2}}\:=\frac{\mathrm{31}\pi}{\mathrm{64}}\:\:{as}\:{approximatevalue}\:{for}\:{this}\:{integra} \\ $$$$\alpha_{\mathrm{0}} \sim\mathrm{1}\:,\mathrm{52}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 25/May/19
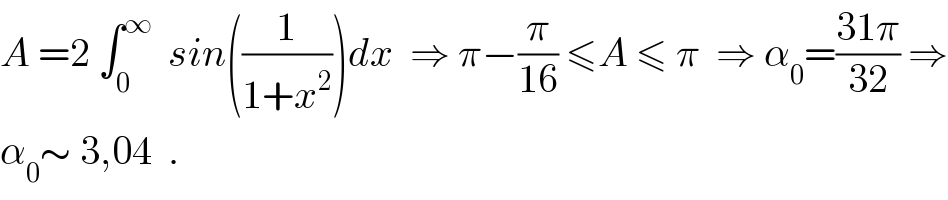
A =2 ∫_0 ^∞ sin((1/(1+x^2 )))dx ⇒ π−(π/(16)) ≤A ≤ π ⇒ α_0 =((31π)/(32)) ⇒ α_0 ∼ 3,04 .
$${A}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:{sin}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}\:\:\Rightarrow\:\pi−\frac{\pi}{\mathrm{16}}\:\leqslant{A}\:\leqslant\:\pi\:\:\Rightarrow\:\alpha_{\mathrm{0}} =\frac{\mathrm{31}\pi}{\mathrm{32}}\:\Rightarrow \\ $$$$\alpha_{\mathrm{0}} \sim\:\mathrm{3},\mathrm{04}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *