Menu Close

sin-1-ax-c-sin-1-bx-c-sin-1-x-When-a-2-b-2-c-2-

Tinku Tara 0 Comments
Pin




Question Number 24098 by Sudipta Jana last updated on 12/Nov/17
sin^(−1) ((ax)/c)+sin^(−1) ((bx)/c)=sin^(−1) x [When a^2 +b^2 =c^2 ]
sin−1axc+sin−1bxc=sin−1x[Whena2+b2=c2]
Answered by 951172235v last updated on 05/Feb/19
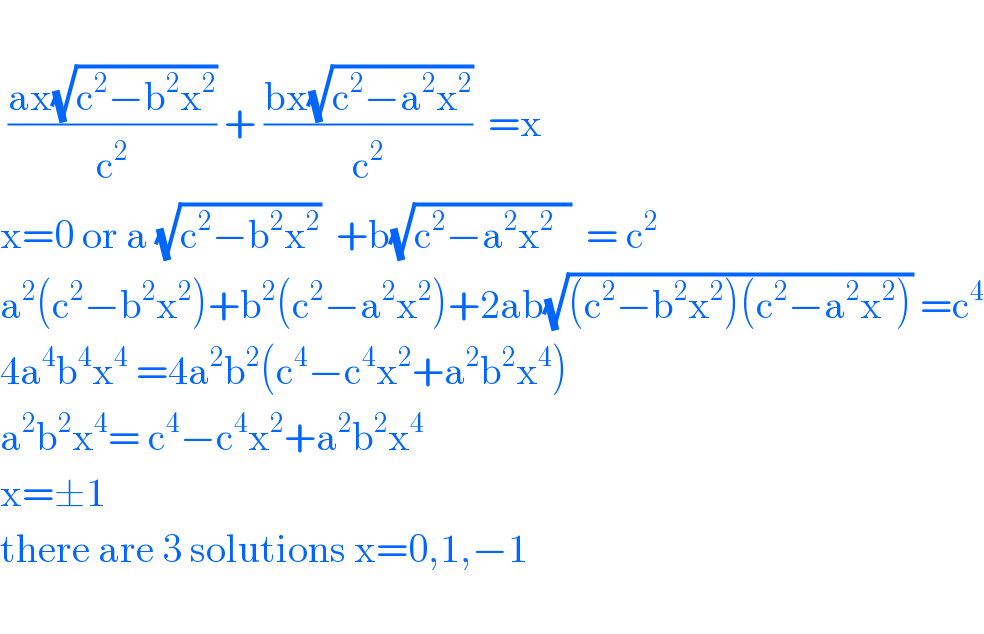
((ax(√(c^2 −b^2 x^2 )))/c^2 ) + ((bx(√(c^2 −a^2 x^2 )))/c^2 ) =x x=0 or a (√(c^2 −b^2 x^2 )) +b(√(c^2 −a^2 x^2 )) = c^2 a^2 (c^2 −b^2 x^2 )+b^2 (c^2 −a^2 x^2 )+2ab(√((c^2 −b^2 x^2 )(c^2 −a^2 x^2 ))) =c^4 4a^4 b^4 x^4 =4a^2 b^2 (c^4 −c^4 x^2 +a^2 b^2 x^4 ) a^2 b^2 x^4 = c^4 −c^4 x^2 +a^2 b^2 x^4 x=±1 there are 3 solutions x=0,1,−1
axc2−b2x2c2+bxc2−a2x2c2=xx=0orac2−b2x2+bc2−a2x2=c2a2(c2−b2x2)+b2(c2−a2x2)+2ab(c2−b2x2)(c2−a2x2)=c44a4b4x4=4a2b2(c4−c4x2+a2b2x4)a2b2x4=c4−c4x2+a2b2x4x=±1thereare3solutionsx=0,1,−1

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *