sin-1-x-2-dx-

Question Number 122877 by bemath last updated on 20/Nov/20

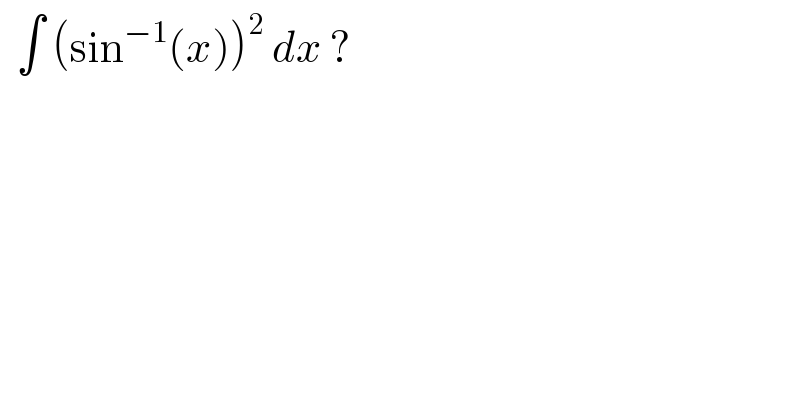
$$\:\:\int\:\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} \:{dx}\:? \\ $$

Commented by liberty last updated on 20/Nov/20

let u = sin^(−1) (x) ⇒x = sin u ⇒ dx = cos u du β(x)=∫ u^2 cos u du =u^2 sin u −2∫u sin u du = u^2 sin u−2(−ucos u +∫ cos u du) = u^2 sin u+2u cos u −2sin u + c = (u^2 −2)sin u +2u cos u + c = x[ (sin^(−1) (x))^2 −2 ]+2sin^(−1) (x) (√(1−x^2 )) + c

$$\:{let}\:{u}\:=\:\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\:\Rightarrow{x}\:=\:\mathrm{sin}\:{u}\: \\ $$$$\Rightarrow\:{dx}\:=\:\mathrm{cos}\:{u}\:{du}\: \\ $$$$\beta\left({x}\right)=\int\:{u}^{\mathrm{2}} \:\mathrm{cos}\:{u}\:{du}\:={u}^{\mathrm{2}} \mathrm{sin}\:{u}\:−\mathrm{2}\int{u}\:\mathrm{sin}\:{u}\:{du} \\ $$$$\:=\:{u}^{\mathrm{2}} \:\mathrm{sin}\:{u}−\mathrm{2}\left(−{u}\mathrm{cos}\:{u}\:+\int\:\mathrm{cos}\:{u}\:{du}\right) \\ $$$$\:=\:{u}^{\mathrm{2}} \:\mathrm{sin}\:{u}+\mathrm{2}{u}\:\mathrm{cos}\:{u}\:−\mathrm{2sin}\:{u}\:+\:{c} \\ $$$$\:=\:\left({u}^{\mathrm{2}} −\mathrm{2}\right)\mathrm{sin}\:{u}\:+\mathrm{2}{u}\:\mathrm{cos}\:{u}\:+\:{c}\: \\ $$$$\:=\:{x}\left[\:\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} −\mathrm{2}\:\right]+\mathrm{2sin}^{−\mathrm{1}} \left({x}\right)\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\:{c}\: \\ $$

Answered by mathmax by abdo last updated on 21/Nov/20

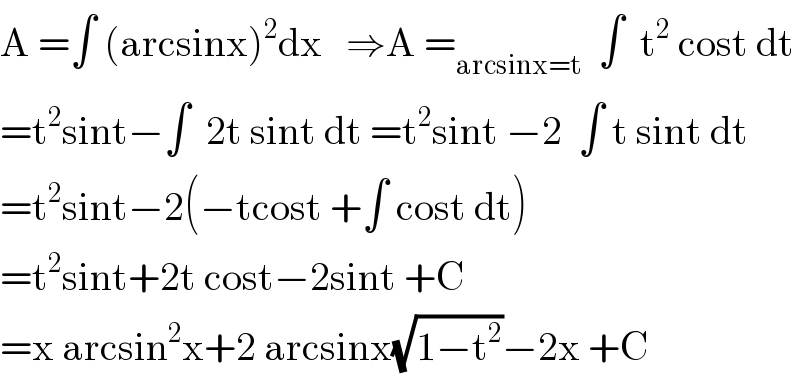
A =∫ (arcsinx)^2 dx ⇒A =_(arcsinx=t) ∫ t^2 cost dt =t^2 sint−∫ 2t sint dt =t^2 sint −2 ∫ t sint dt =t^2 sint−2(−tcost +∫ cost dt) =t^2 sint+2t cost−2sint +C =x arcsin^2 x+2 arcsinx(√(1−t^2 ))−2x +C

$$\mathrm{A}\:=\int\:\left(\mathrm{arcsinx}\right)^{\mathrm{2}} \mathrm{dx}\:\:\:\Rightarrow\mathrm{A}\:=_{\mathrm{arcsinx}=\mathrm{t}} \:\:\int\:\:\mathrm{t}^{\mathrm{2}} \:\mathrm{cost}\:\mathrm{dt} \\ $$$$=\mathrm{t}^{\mathrm{2}} \mathrm{sint}−\int\:\:\mathrm{2t}\:\mathrm{sint}\:\mathrm{dt}\:=\mathrm{t}^{\mathrm{2}} \mathrm{sint}\:−\mathrm{2}\:\:\int\:\mathrm{t}\:\mathrm{sint}\:\mathrm{dt} \\ $$$$=\mathrm{t}^{\mathrm{2}} \mathrm{sint}−\mathrm{2}\left(−\mathrm{tcost}\:+\int\:\mathrm{cost}\:\mathrm{dt}\right) \\ $$$$=\mathrm{t}^{\mathrm{2}} \mathrm{sint}+\mathrm{2t}\:\mathrm{cost}−\mathrm{2sint}\:+\mathrm{C} \\ $$$$=\mathrm{x}\:\mathrm{arcsin}^{\mathrm{2}} \mathrm{x}+\mathrm{2}\:\mathrm{arcsinx}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }−\mathrm{2x}\:+\mathrm{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply