Question Number 39231 by LX Z last updated on 04/Jul/18

$$\left({sin}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} +\:\:\left({sin}^{−\mathrm{1}} {y}\right)^{\mathrm{2}} +\:\:\mathrm{2}\left({sin}^{−\mathrm{1}} {x}\right) \\ $$$$\left({sin}^{−\mathrm{1}} {y}\right)=\:\pi^{\mathrm{2}} ,{then}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:{is}\:{equal}\:{to}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jul/18
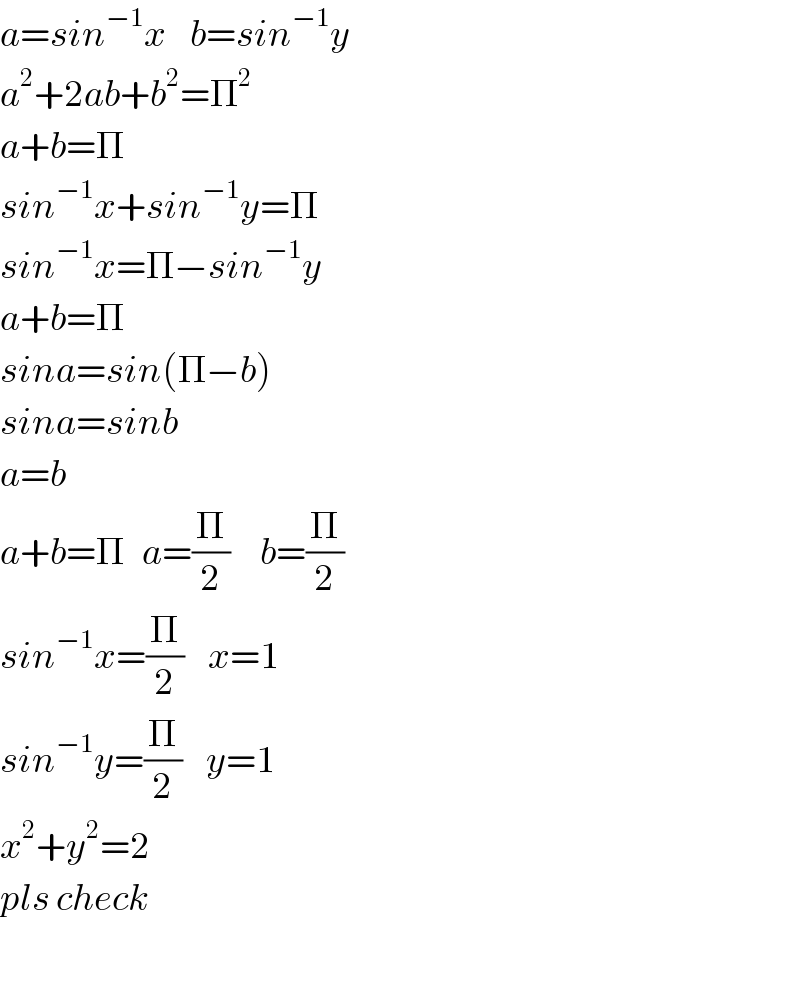
$${a}={sin}^{−\mathrm{1}} {x}\:\:\:\:{b}={sin}^{−\mathrm{1}} {y}\:\:\:\:\: \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} =\prod^{\mathrm{2}} \\ $$$${a}+{b}=\Pi \\ $$$${sin}^{−\mathrm{1}} {x}+{sin}^{−\mathrm{1}} {y}=\Pi \\ $$$${sin}^{−\mathrm{1}} {x}=\Pi−{sin}^{−\mathrm{1}} {y} \\ $$$${a}+{b}=\Pi \\ $$$${sina}={sin}\left(\Pi−{b}\right) \\ $$$${sina}={sinb} \\ $$$${a}={b}\:\:\: \\ $$$${a}+{b}=\Pi\:\:\:{a}=\frac{\Pi}{\mathrm{2}}\:\:\:\:\:{b}=\frac{\Pi}{\mathrm{2}} \\ $$$${sin}^{−\mathrm{1}} {x}=\frac{\Pi}{\mathrm{2}}\:\:\:\:{x}=\mathrm{1} \\ $$$${sin}^{−\mathrm{1}} {y}=\frac{\Pi}{\mathrm{2}}\:\:\:\:{y}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2} \\ $$$${pls}\:{check}\: \\ $$$$ \\ $$
