Menu Close

sin-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 117910 by bemath last updated on 14/Oct/20
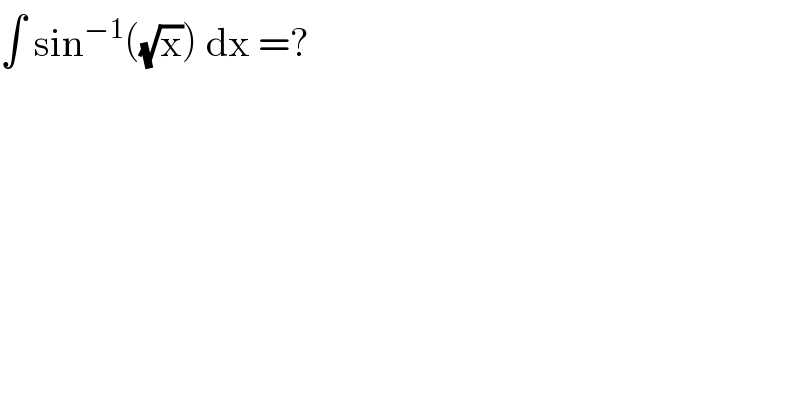
∫ sin^(−1) ((√x)) dx =?
$$\int\:\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\:=? \\ $$
Commented by bemath last updated on 14/Oct/20
Answered by Lordose last updated on 14/Oct/20
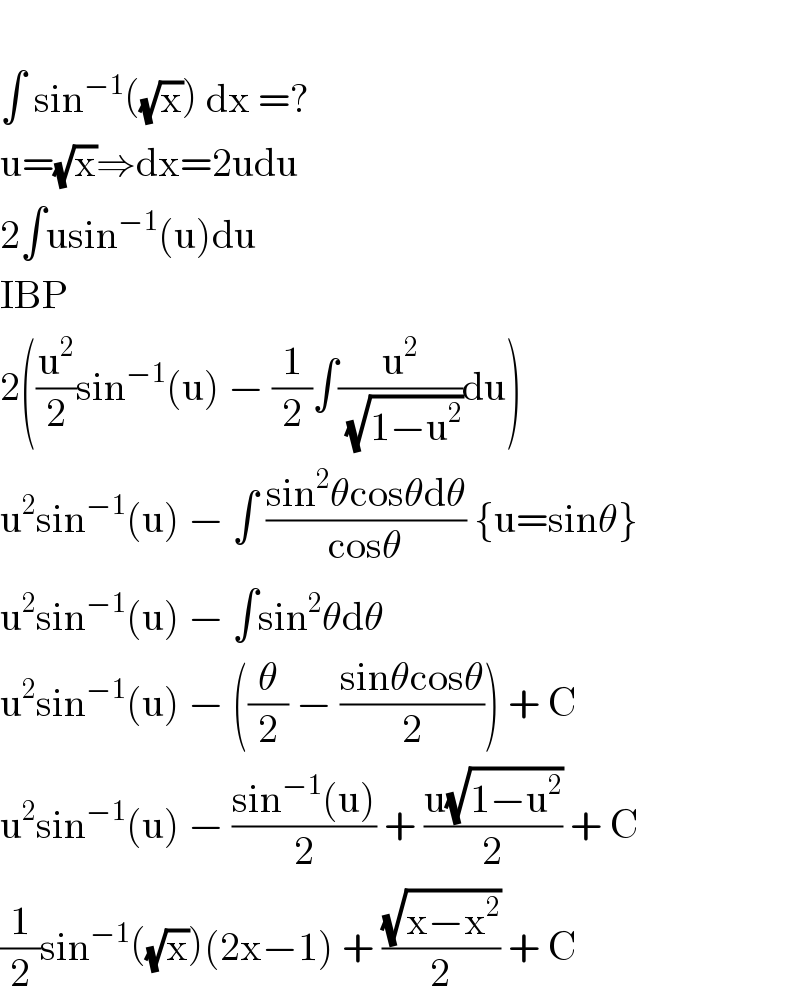
∫ sin^(−1) ((√x)) dx =? u=(√x)⇒dx=2udu 2∫usin^(−1) (u)du IBP 2((u^2 /2)sin^(−1) (u) − (1/2)∫(u^2 /( (√(1−u^2 ))))du) u^2 sin^(−1) (u) − ∫ ((sin^2 θcosθdθ)/(cosθ)) {u=sinθ} u^2 sin^(−1) (u) − ∫sin^2 θdθ u^2 sin^(−1) (u) − ((θ/2) − ((sinθcosθ)/2)) + C u^2 sin^(−1) (u) − ((sin^(−1) (u))/2) + ((u(√(1−u^2 )))/2) + C (1/2)sin^(−1) ((√x))(2x−1) + ((√(x−x^2 ))/2) + C
$$ \\ $$$$\int\:\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\:=? \\ $$$$\mathrm{u}=\sqrt{\mathrm{x}}\Rightarrow\mathrm{dx}=\mathrm{2udu} \\ $$$$\mathrm{2}\int\mathrm{usin}^{−\mathrm{1}} \left(\mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{IBP} \\ $$$$\mathrm{2}\left(\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)\:−\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{u}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\mathrm{du}\right) \\ $$$$\mathrm{u}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)\:−\:\int\:\frac{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}\theta\mathrm{d}\theta}{\mathrm{cos}\theta}\:\left\{\mathrm{u}=\mathrm{sin}\theta\right\} \\ $$$$\mathrm{u}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)\:−\:\int\mathrm{sin}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\mathrm{u}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)\:−\:\left(\frac{\theta}{\mathrm{2}}\:−\:\frac{\mathrm{sin}\theta\mathrm{cos}\theta}{\mathrm{2}}\right)\:+\:\mathrm{C} \\ $$$$\mathrm{u}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)\:−\:\frac{\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{u}\right)}{\mathrm{2}}\:+\:\frac{\mathrm{u}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}{\mathrm{2}}\:+\:\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\left(\mathrm{2x}−\mathrm{1}\right)\:+\:\frac{\sqrt{\mathrm{x}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{2}}\:+\:\mathrm{C} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Oct/20
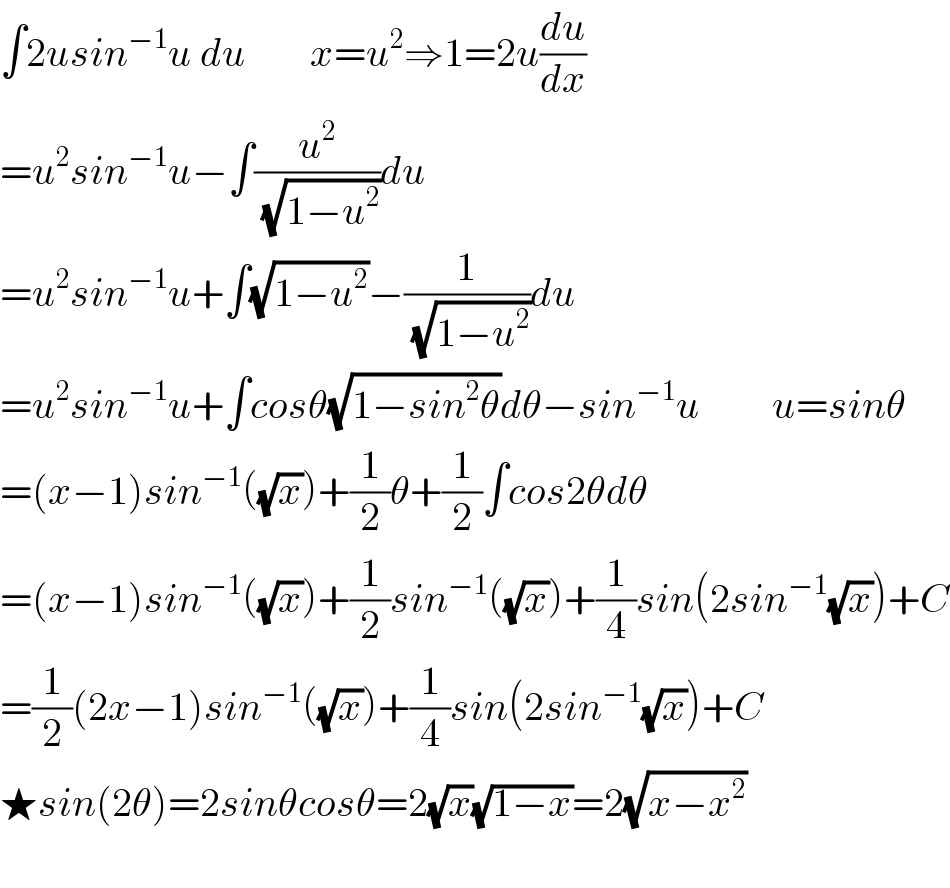
∫2usin^(−1) u du x=u^2 ⇒1=2u(du/dx) =u^2 sin^(−1) u−∫(u^2 /( (√(1−u^2 ))))du =u^2 sin^(−1) u+∫(√(1−u^2 ))−(1/( (√(1−u^2 ))))du =u^2 sin^(−1) u+∫cosθ(√(1−sin^2 θ))dθ−sin^(−1) u u=sinθ =(x−1)sin^(−1) ((√x))+(1/2)θ+(1/2)∫cos2θdθ =(x−1)sin^(−1) ((√x))+(1/2)sin^(−1) ((√x))+(1/4)sin(2sin^(−1) (√x))+C =(1/2)(2x−1)sin^(−1) ((√x))+(1/4)sin(2sin^(−1) (√x))+C ★sin(2θ)=2sinθcosθ=2(√x)(√(1−x))=2(√(x−x^2 ))
$$\int\mathrm{2}{usin}^{−\mathrm{1}} {u}\:{du}\:\:\:\:\:\:\:\:{x}={u}^{\mathrm{2}} \Rightarrow\mathrm{1}=\mathrm{2}{u}\frac{{du}}{{dx}} \\ $$$$={u}^{\mathrm{2}} {sin}^{−\mathrm{1}} {u}−\int\frac{{u}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du} \\ $$$$={u}^{\mathrm{2}} {sin}^{−\mathrm{1}} {u}+\int\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du} \\ $$$$={u}^{\mathrm{2}} {sin}^{−\mathrm{1}} {u}+\int{cos}\theta\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}{d}\theta−{sin}^{−\mathrm{1}} {u}\:\:\:\:\:\:\:\:\:{u}={sin}\theta \\ $$$$=\left({x}−\mathrm{1}\right){sin}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\theta+\frac{\mathrm{1}}{\mathrm{2}}\int{cos}\mathrm{2}\theta{d}\theta \\ $$$$=\left({x}−\mathrm{1}\right){sin}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{sin}^{−\mathrm{1}} \sqrt{{x}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}−\mathrm{1}\right){sin}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{sin}^{−\mathrm{1}} \sqrt{{x}}\right)+{C} \\ $$$$\bigstar{sin}\left(\mathrm{2}\theta\right)=\mathrm{2}{sin}\theta{cos}\theta=\mathrm{2}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}=\mathrm{2}\sqrt{{x}−{x}^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 14/Oct/20
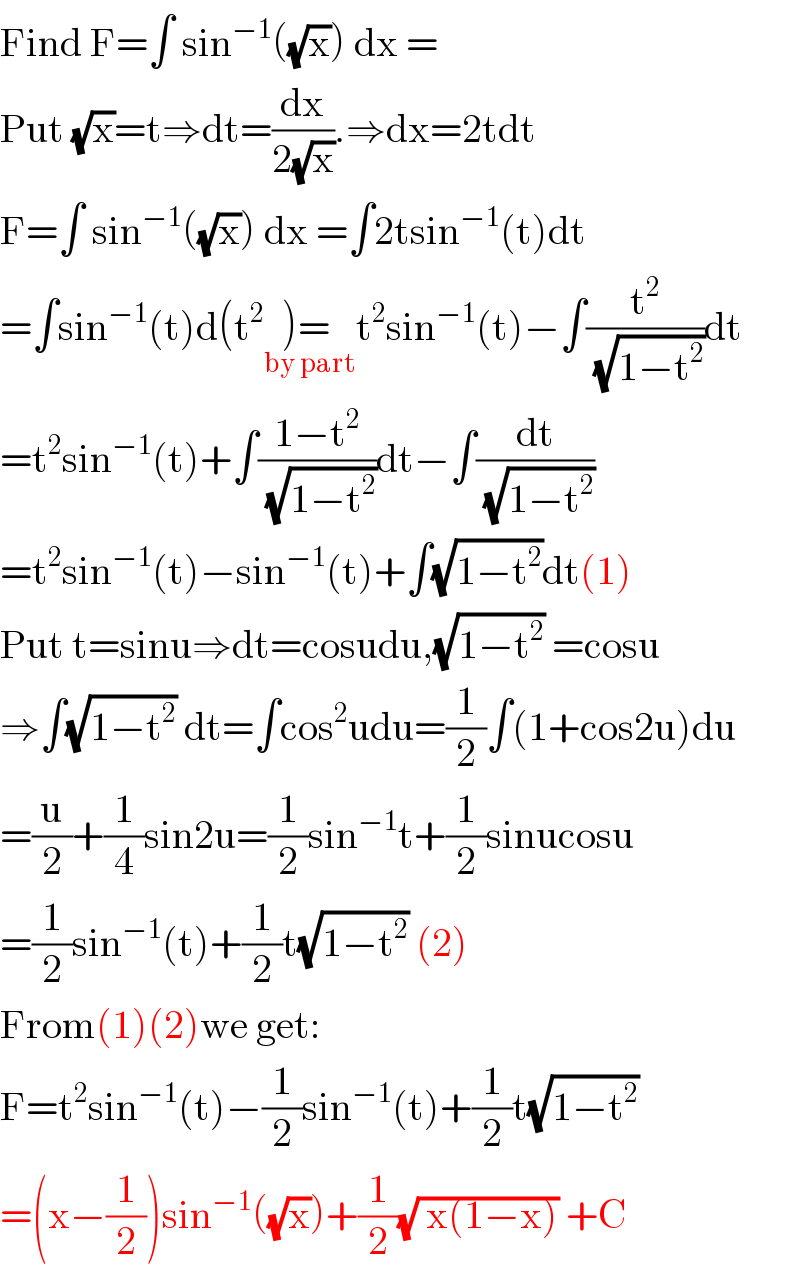
Find F=∫ sin^(−1) ((√x)) dx = Put (√x)=t⇒dt=(dx/(2(√x))).⇒dx=2tdt F=∫ sin^(−1) ((√x)) dx =∫2tsin^(−1) (t)dt =∫sin^(−1) (t)d(t^2 )= _(by part) t^2 sin^(−1) (t)−∫(t^2 /( (√(1−t^2 ))))dt =t^2 sin^(−1) (t)+∫((1−t^2 )/( (√(1−t^2 ))))dt−∫(dt/( (√(1−t^2 )))) =t^2 sin^(−1) (t)−sin^(−1) (t)+∫(√(1−t^2 ))dt(1) Put t=sinu⇒dt=cosudu,(√(1−t^2 )) =cosu ⇒∫(√(1−t^2 )) dt=∫cos^2 udu=(1/2)∫(1+cos2u)du =(u/2)+(1/4)sin2u=(1/2)sin^(−1) t+(1/2)sinucosu =(1/2)sin^(−1) (t)+(1/2)t(√(1−t^2 )) (2) From(1)(2)we get: F=t^2 sin^(−1) (t)−(1/2)sin^(−1) (t)+(1/2)t(√(1−t^2 )) =(x−(1/2))sin^(−1) ((√x))+(1/2)(√( x(1−x))) +C
$$\mathrm{Find}\:\mathrm{F}=\int\:\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\:= \\ $$$$\mathrm{Put}\:\sqrt{\mathrm{x}}=\mathrm{t}\Rightarrow\mathrm{dt}=\frac{\mathrm{dx}}{\mathrm{2}\sqrt{\mathrm{x}}}.\Rightarrow\mathrm{dx}=\mathrm{2tdt} \\ $$$$\mathrm{F}=\int\:\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\:=\int\mathrm{2tsin}^{−\mathrm{1}} \left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)\mathrm{d}\left(\mathrm{t}^{\mathrm{2}} \underset{\mathrm{by}\:\mathrm{part}} {\right)=\:}\mathrm{t}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)−\int\frac{\mathrm{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\mathrm{dt} \\ $$$$=\mathrm{t}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)+\int\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}−\int\frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }} \\ $$$$=\mathrm{t}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)+\int\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\left(\mathrm{1}\right) \\ $$$$\mathrm{Put}\:\mathrm{t}=\mathrm{sinu}\Rightarrow\mathrm{dt}=\mathrm{cosudu},\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:=\mathrm{cosu} \\ $$$$\Rightarrow\int\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}=\int\mathrm{cos}^{\mathrm{2}} \mathrm{udu}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}+\mathrm{cos2u}\right)\mathrm{du} \\ $$$$=\frac{\mathrm{u}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin2u}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinucosu} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\mathrm{1}\right)\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{F}=\mathrm{t}^{\mathrm{2}} \mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} } \\ $$$$=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\:\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)}\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *