Question Number 117724 by bemath last updated on 13/Oct/20
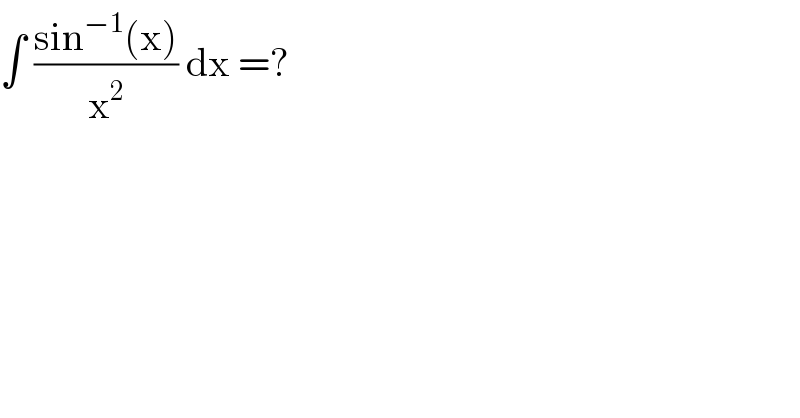
$$\int\:\frac{\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=? \\ $$
Commented by MJS_new last updated on 13/Oct/20
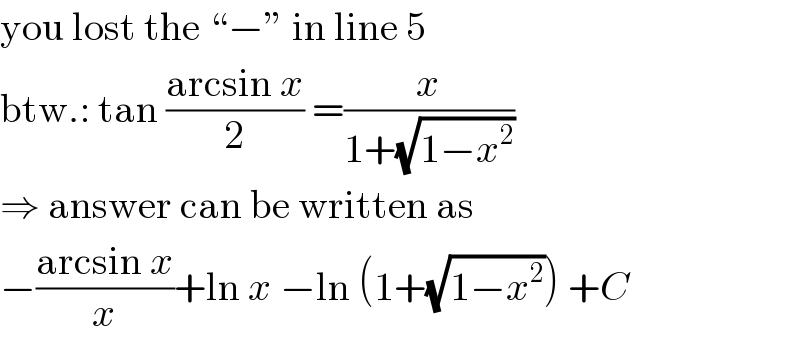
$$\mathrm{you}\:\mathrm{lost}\:\mathrm{the}\:“−''\:\mathrm{in}\:\mathrm{line}\:\mathrm{5} \\ $$$$\mathrm{btw}.:\:\mathrm{tan}\:\frac{\mathrm{arcsin}\:{x}}{\mathrm{2}}\:=\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$$−\frac{\mathrm{arcsin}\:{x}}{{x}}+\mathrm{ln}\:{x}\:−\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:+{C} \\ $$
Commented by MJS_new last updated on 13/Oct/20
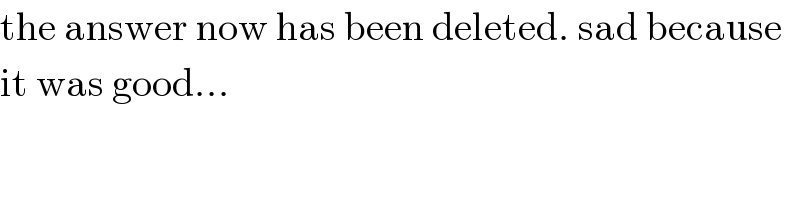
$$\mathrm{the}\:\mathrm{answer}\:\mathrm{now}\:\mathrm{has}\:\mathrm{been}\:\mathrm{deleted}.\:\mathrm{sad}\:\mathrm{because} \\ $$$$\mathrm{it}\:\mathrm{was}\:\mathrm{good}… \\ $$
Commented by bemath last updated on 13/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by bemath last updated on 13/Oct/20

$$\mathrm{in}\:\mathrm{line}\:\mathrm{5}\:\mathrm{sir}? \\ $$
Commented by bemath last updated on 13/Oct/20
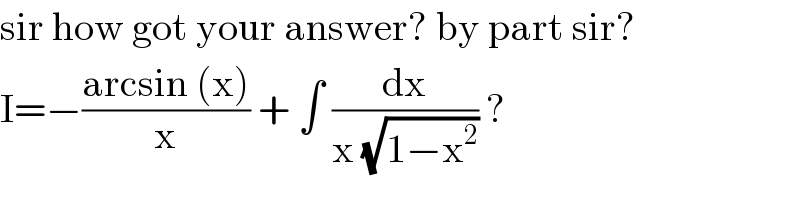
$$\mathrm{sir}\:\mathrm{how}\:\mathrm{got}\:\mathrm{your}\:\mathrm{answer}?\:\mathrm{by}\:\mathrm{part}\:\mathrm{sir}? \\ $$$$\mathrm{I}=−\frac{\mathrm{arcsin}\:\left(\mathrm{x}\right)}{\mathrm{x}}\:+\:\int\:\frac{\mathrm{dx}}{\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:? \\ $$
Answered by MJS_new last updated on 13/Oct/20
![∫((arcsin x)/x^2 )dx= [by parts] =−((arcsin x)/x)+∫(dx/(x(√(1−x^2 ))))= [t=sin x → dx=(√(1−x^2 ))dt] =−((arcsin x)/x)+∫(dt/(sin t))= =−((arcsin x)/x)+ln tan (t/2) = =−((arcsin x)/x)+ln tan ((arcsin x)/2) = =−((arcsin x)/x)+ln ∣x∣ −ln (1+(√(1−x^2 ))) +C](https://www.tinkutara.com/question/Q117750.png)
$$\int\frac{\mathrm{arcsin}\:{x}}{{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=−\frac{\mathrm{arcsin}\:{x}}{{x}}+\int\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dt}\right] \\ $$$$=−\frac{\mathrm{arcsin}\:{x}}{{x}}+\int\frac{{dt}}{\mathrm{sin}\:{t}}= \\ $$$$=−\frac{\mathrm{arcsin}\:{x}}{{x}}+\mathrm{ln}\:\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\:= \\ $$$$=−\frac{\mathrm{arcsin}\:{x}}{{x}}+\mathrm{ln}\:\mathrm{tan}\:\frac{\mathrm{arcsin}\:{x}}{\mathrm{2}}\:= \\ $$$$=−\frac{\mathrm{arcsin}\:{x}}{{x}}+\mathrm{ln}\:\mid{x}\mid\:−\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:+{C} \\ $$
Commented by bemath last updated on 13/Oct/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by Bird last updated on 14/Oct/20

$${by}\:{parts}\:\int\:\frac{{arcsinx}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{{arcsinx}}{{x}}+\int\:\frac{\mathrm{1}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:{but} \\ $$$$\int\:\frac{{dx}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=_{{x}={sint}} \:\:\:\int\:\frac{{cost}}{{sintcost}}{dt} \\ $$$$=\int\:\frac{{dt}}{{sint}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={z}} \:\:\int\frac{\mathrm{2}{dz}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\frac{\mathrm{2}{z}}{\mathrm{1}+{z}^{\mathrm{2}} }} \\ $$$$=\int\:\frac{{dz}}{{z}}\:\:={ln}\mid{z}\mid\:+{c}\:={ln}\mid{tan}\left(\frac{{t}}{\mathrm{2}}\right)\mid+{c} \\ $$$$={ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsinx}\right)\mid\:+{c}\:\Rightarrow \\ $$$${I}\:=−\frac{{arcsinx}}{{x}}+{ln}\mid{tan}\left(\frac{{arcsinx}}{\mathrm{2}}\right)\mid+{c} \\ $$$$ \\ $$
