Question Number 83266 by 09658867628 last updated on 29/Feb/20
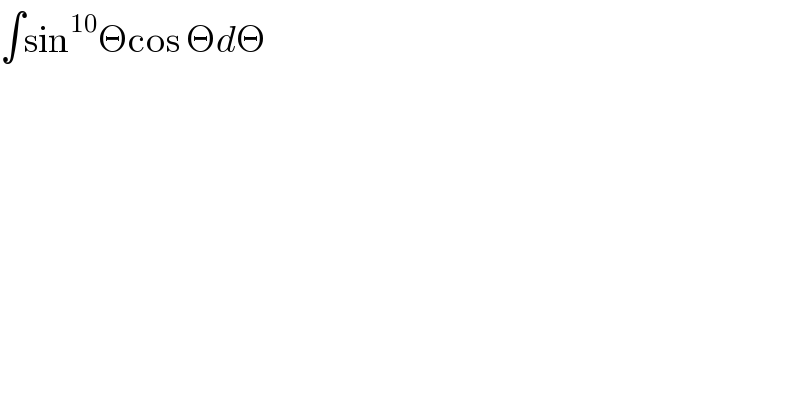
$$\int\mathrm{sin}^{\mathrm{10}} \Theta\mathrm{cos}\:\Theta{d}\Theta\: \\ $$
Commented by Tony Lin last updated on 29/Feb/20
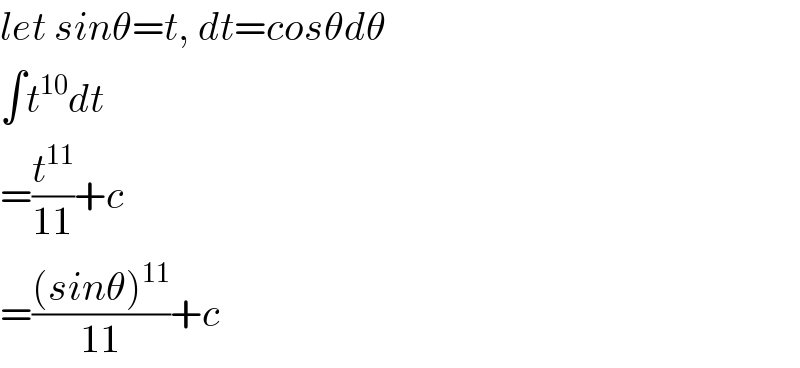
$${let}\:{sin}\theta={t},\:{dt}={cos}\theta{d}\theta \\ $$$$\int{t}^{\mathrm{10}} {dt} \\ $$$$=\frac{{t}^{\mathrm{11}} }{\mathrm{11}}+{c} \\ $$$$=\frac{\left({sin}\theta\right)^{\mathrm{11}} }{\mathrm{11}}+{c} \\ $$
Answered by Rio Michael last updated on 29/Feb/20

$$−−−−−−−−−− \\ $$$$\boldsymbol{\mathrm{solution}} \\ $$$$\int\mathrm{sin}\:^{\mathrm{10}} \theta\:\mathrm{cos}\:\theta\:{d}\theta \\ $$$$\mathrm{let}\:\mathrm{sin}\theta\:=\:{u}\:\Rightarrow\:\frac{{du}}{{d}\theta}\:=\:\mathrm{cos}\theta \\ $$$$\therefore\:{d}\theta\:=\:\frac{{du}}{\mathrm{cos}\theta} \\ $$$$\Rightarrow\:\int\mathrm{sin}^{\mathrm{10}} \theta\mathrm{cos}\theta\:{d}\theta\:=\:\int{u}^{\mathrm{10}} \:\mathrm{cos}\theta\:\frac{{du}}{\mathrm{cos}\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int{u}^{\mathrm{10}} {du}\:=\:\frac{{u}^{\mathrm{11}} }{\mathrm{11}}\:+\:{k} \\ $$$$\Rightarrow\:\int\mathrm{sin}^{\mathrm{10}} \theta\:\mathrm{cos}\theta\:{d}\theta\:=\:\frac{\mathrm{sin}^{\mathrm{11}} \theta}{\mathrm{11}}\:+\:{k} \\ $$
