Menu Close

sin-101x-sin-99-xdx-

Tinku Tara 0 Comments
Pin




Question Number 23830 by anunil1234 last updated on 07/Nov/17
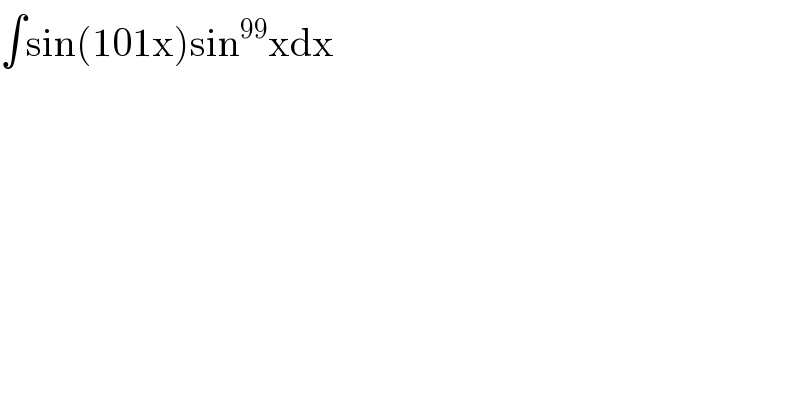
∫sin(101x)sin^(99) xdx
$$\int\mathrm{sin}\left(\mathrm{101x}\right)\mathrm{sin}^{\mathrm{99}} \mathrm{xdx} \\ $$
Commented by prakash jain last updated on 07/Nov/17
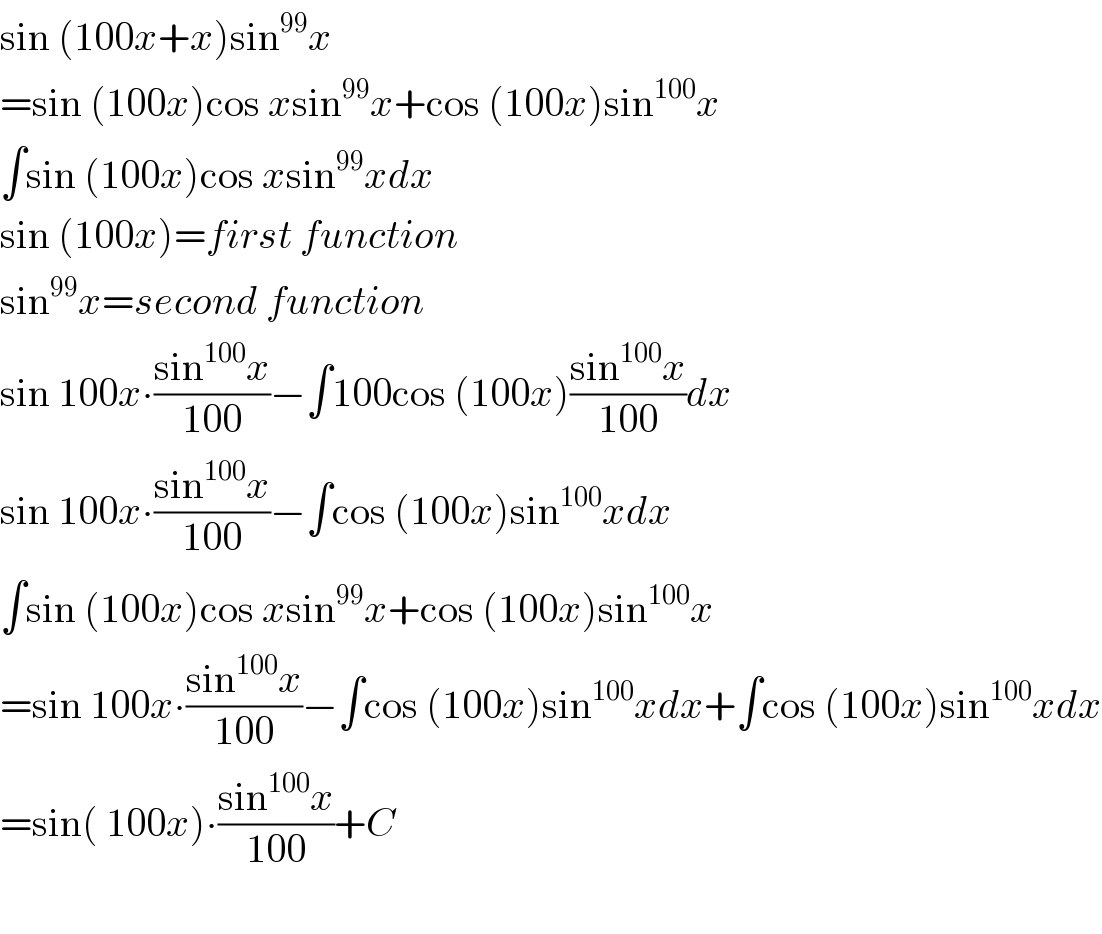
sin (100x+x)sin^(99) x =sin (100x)cos xsin^(99) x+cos (100x)sin^(100) x ∫sin (100x)cos xsin^(99) xdx sin (100x)=first function sin^(99) x=second function sin 100x∙((sin^(100) x)/(100))−∫100cos (100x)((sin^(100) x)/(100))dx sin 100x∙((sin^(100) x)/(100))−∫cos (100x)sin^(100) xdx ∫sin (100x)cos xsin^(99) x+cos (100x)sin^(100) x =sin 100x∙((sin^(100) x)/(100))−∫cos (100x)sin^(100) xdx+∫cos (100x)sin^(100) xdx =sin( 100x)∙((sin^(100) x)/(100))+C
$$\mathrm{sin}\:\left(\mathrm{100}{x}+{x}\right)\mathrm{sin}^{\mathrm{99}} {x} \\ $$$$=\mathrm{sin}\:\left(\mathrm{100}{x}\right)\mathrm{cos}\:{x}\mathrm{sin}^{\mathrm{99}} {x}+\mathrm{cos}\:\left(\mathrm{100}{x}\right)\mathrm{sin}^{\mathrm{100}} {x} \\ $$$$\int\mathrm{sin}\:\left(\mathrm{100}{x}\right)\mathrm{cos}\:{x}\mathrm{sin}^{\mathrm{99}} {xdx} \\ $$$$\mathrm{sin}\:\left(\mathrm{100}{x}\right)={first}\:{function} \\ $$$$\mathrm{sin}^{\mathrm{99}} {x}={second}\:{function} \\ $$$$\mathrm{sin}\:\mathrm{100}{x}\centerdot\frac{\mathrm{sin}^{\mathrm{100}} {x}}{\mathrm{100}}−\int\mathrm{100cos}\:\left(\mathrm{100}{x}\right)\frac{\mathrm{sin}^{\mathrm{100}} {x}}{\mathrm{100}}{dx} \\ $$$$\mathrm{sin}\:\mathrm{100}{x}\centerdot\frac{\mathrm{sin}^{\mathrm{100}} {x}}{\mathrm{100}}−\int\mathrm{cos}\:\left(\mathrm{100}{x}\right)\mathrm{sin}^{\mathrm{100}} {xdx} \\ $$$$\int\mathrm{sin}\:\left(\mathrm{100}{x}\right)\mathrm{cos}\:{x}\mathrm{sin}^{\mathrm{99}} {x}+\mathrm{cos}\:\left(\mathrm{100}{x}\right)\mathrm{sin}^{\mathrm{100}} {x} \\ $$$$=\mathrm{sin}\:\mathrm{100}{x}\centerdot\frac{\mathrm{sin}^{\mathrm{100}} {x}}{\mathrm{100}}−\int\mathrm{cos}\:\left(\mathrm{100}{x}\right)\mathrm{sin}^{\mathrm{100}} {xdx}+\int\mathrm{cos}\:\left(\mathrm{100}{x}\right)\mathrm{sin}^{\mathrm{100}} {xdx} \\ $$$$=\mathrm{sin}\left(\:\mathrm{100}{x}\right)\centerdot\frac{\mathrm{sin}^{\mathrm{100}} {x}}{\mathrm{100}}+{C} \\ $$$$ \\ $$
Commented by anunil1234 last updated on 08/Nov/17
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *