Question Number 166360 by mathlove last updated on 19/Feb/22
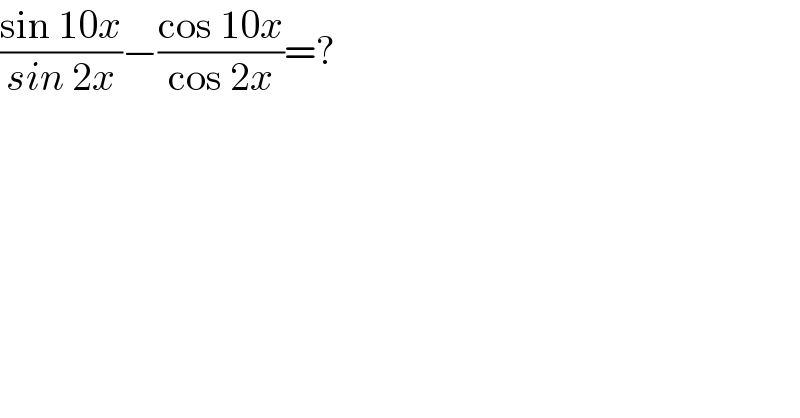
$$\frac{\mathrm{sin}\:\mathrm{10}{x}}{{sin}\:\mathrm{2}{x}}−\frac{\mathrm{cos}\:\mathrm{10}{x}}{\mathrm{cos}\:\mathrm{2}{x}}=? \\ $$
Answered by som(math1967) last updated on 19/Feb/22
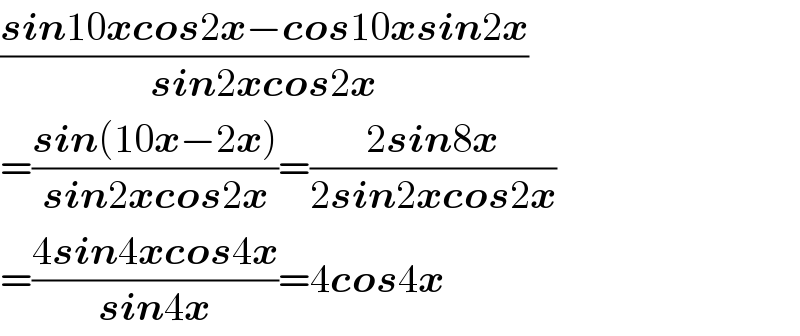
$$\frac{\boldsymbol{{sin}}\mathrm{10}\boldsymbol{{xcos}}\mathrm{2}\boldsymbol{{x}}−\boldsymbol{{cos}}\mathrm{10}\boldsymbol{{xsin}}\mathrm{2}\boldsymbol{{x}}}{\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{xcos}}\mathrm{2}\boldsymbol{{x}}} \\ $$$$=\frac{\boldsymbol{{sin}}\left(\mathrm{10}\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{x}}\right)}{\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{xcos}}\mathrm{2}\boldsymbol{{x}}}=\frac{\mathrm{2}\boldsymbol{{sin}}\mathrm{8}\boldsymbol{{x}}}{\mathrm{2}\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{xcos}}\mathrm{2}\boldsymbol{{x}}} \\ $$$$=\frac{\mathrm{4}\boldsymbol{{sin}}\mathrm{4}\boldsymbol{{xcos}}\mathrm{4}\boldsymbol{{x}}}{\boldsymbol{{sin}}\mathrm{4}\boldsymbol{{x}}}=\mathrm{4}\boldsymbol{{cos}}\mathrm{4}\boldsymbol{{x}} \\ $$
Commented by mathlove last updated on 19/Feb/22

$${thanks} \\ $$
