Question Number 29821 by Victor31926 last updated on 12/Feb/18

$$\frac{\mathrm{sin}\:\mathrm{16x}}{\mathrm{sin}\:\mathrm{x}}\:\:\:\:\:\:?\mathrm{pls}\:\mathrm{help}. \\ $$
Commented by abdo imad last updated on 13/Feb/18
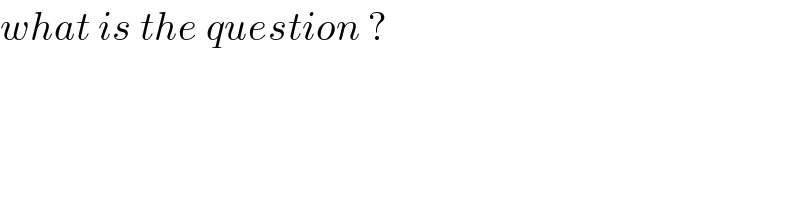
$${what}\:{is}\:{the}\:{question}\:? \\ $$
Commented by MJS last updated on 14/Feb/18
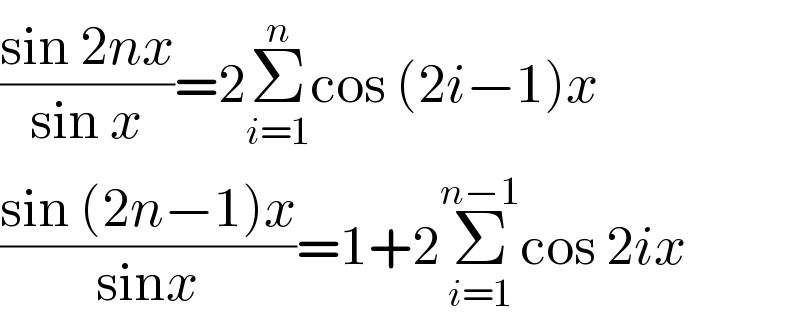
$$\frac{\mathrm{sin}\:\mathrm{2}{nx}}{\mathrm{sin}\:{x}}=\mathrm{2}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\:\left(\mathrm{2}{i}−\mathrm{1}\right){x} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{2}{n}−\mathrm{1}\right){x}}{\mathrm{sin}{x}}=\mathrm{1}+\mathrm{2}\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\mathrm{cos}\:\mathrm{2}{ix} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Feb/18
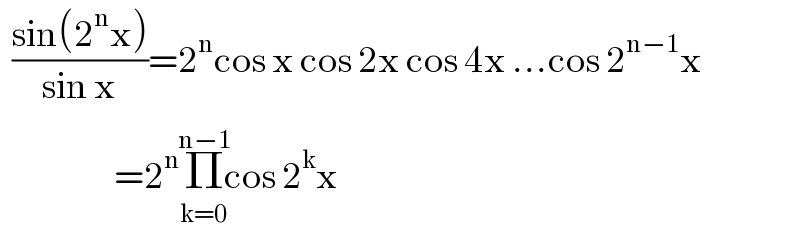
$$\:\:\frac{\mathrm{sin}\left(\mathrm{2}^{\mathrm{n}} \mathrm{x}\right)}{\mathrm{sin}\:\mathrm{x}}=\mathrm{2}^{\mathrm{n}} \mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{4x}\:…\mathrm{cos}\:\mathrm{2}^{\mathrm{n}−\mathrm{1}} \mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{n}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\Pi}}\mathrm{cos}\:\mathrm{2}^{\mathrm{k}} \mathrm{x} \\ $$
Answered by Rasheed.Sindhi last updated on 12/Feb/18
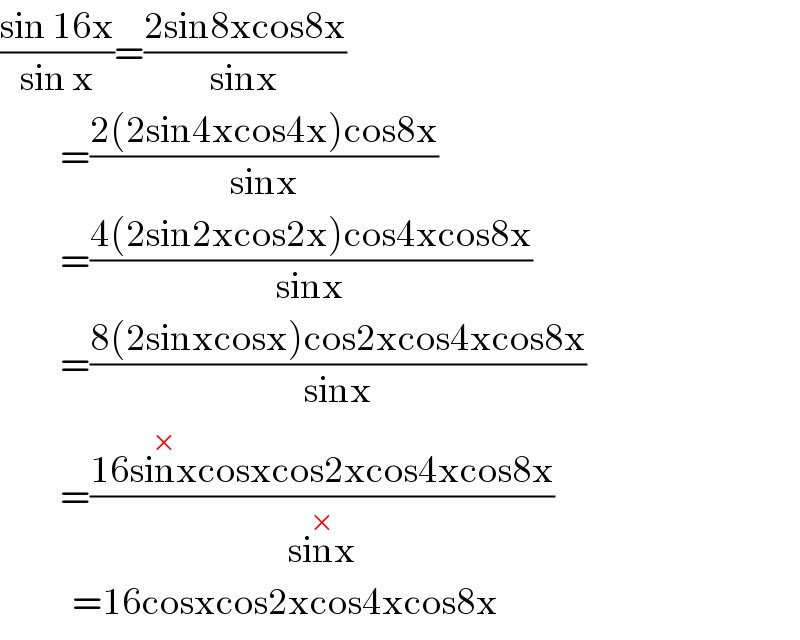
$$\frac{\mathrm{sin}\:\mathrm{16x}}{\mathrm{sin}\:\mathrm{x}}=\frac{\mathrm{2sin8xcos8x}}{\mathrm{sinx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\left(\mathrm{2sin4xcos4x}\right)\mathrm{cos8x}}{\mathrm{sinx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}\left(\mathrm{2sin2xcos2x}\right)\mathrm{cos4xcos8x}}{\mathrm{sinx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{8}\left(\mathrm{2sinxcosx}\right)\mathrm{cos2xcos4xcos8x}}{\mathrm{sinx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{16}\overset{×} {\mathrm{sinx}cosxcos2xcos4xcos8x}}{\overset{×} {\mathrm{sinx}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{16cosxcos2xcos4xcos8x} \\ $$
Commented by Victor31926 last updated on 12/Feb/18
$$\mathrm{thnks}\:\mathrm{a}\:\mathrm{lot}…\mathrm{are}\:\mathrm{u}\:\mathrm{sure}\:\mathrm{of}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{sir}? \\ $$
